CSG
CSG Operations
There are three binary csg operations which can construct extremely complex objects from very simple primitives: union ($\cup$), intersection ($\cap$) and subtraction (i.e. difference).
This diagram shows the basic idea: 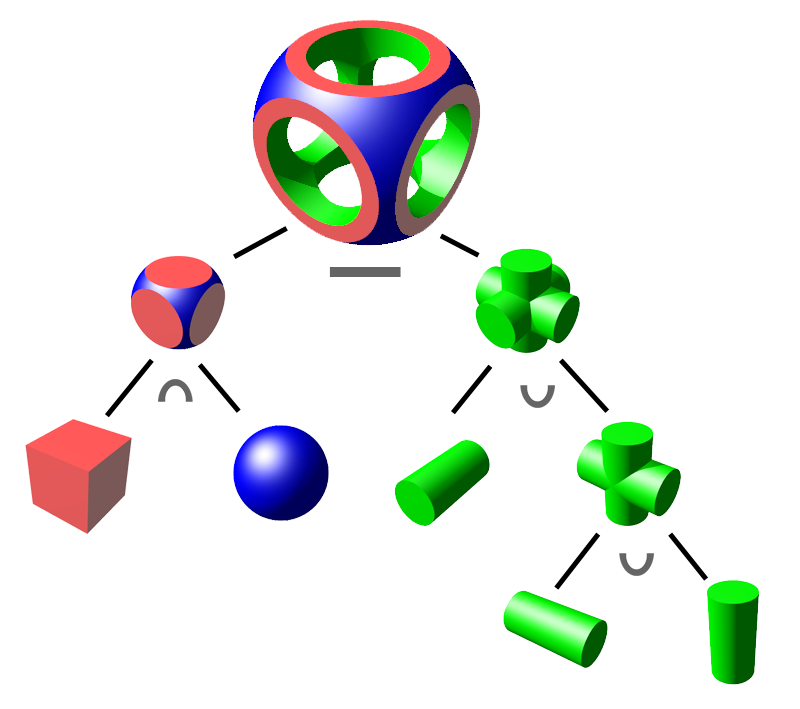
The code for this in our system would look this this:
cyl = Cylinder(0.7)
cyl_cross = csgunion(csgunion(leaf(cyl), leaf(cyl, rotationd(90, 0, 0))), leaf(cyl, rotationd(0, 90, 0)))
cube = Cuboid(1.0, 1.0, 1.0)
sph = Sphere(1.3)
rounded_cube = csgintersection(cube, sph)
result = csgdifference(rounded_cube, cyl_cross)
Vis.draw(result, numdivisions=100)GLMakie.Screen(...)

OpticSim.leaf — Functionleaf(surf::ParametricSurface{T}, transform::RigidBodyTransform{T} = identitytransform(T)) -> CSGGenerator{T}Create a leaf node from a parametric surface with a given transform.
leaf(surf::CSGGenerator{T}, transform::RigidBodyTransform{T} = identitytransform(T)) -> CSGGenerator{T}Create a (pseudo) leaf node from another CSGGenerator, this is useful if you want multiple copies of a premade CSG structure with different transforms, for example in an MLA.
OpticSim.csgunion — Functioncsgunion(a::CSGGenerator{T}, b::CSGGenerator{T}, transform::RigidBodyTransform{T} = identitytransform(T)) -> CSGGenerator{T}Create a binary node in the CSG tree representing a union between a and b. A shortcut method for a and b as ParametricSurfaces is also available.
OpticSim.csgintersection — Functioncsgintersection(a::CSGGenerator{T} b::CSGGenerator{T}, transform::RigidBodyTransform{T} = identitytransform(T)) -> CSGGenerator{T}Create a binary node in the CSG tree representing an intersection between a and b. A shortcut method for a and b as ParametricSurfaces is also available.
OpticSim.csgdifference — Functioncsgdifference(a::CSGGenerator{T}, b::CSGGenerator{T}, transform::RigidBodyTransform{T} = identitytransform(T)) -> CSGGenerator{T}Create a binary node in the CSG tree representing the difference of a and b, essentially a - b. A shortcut method for a and b as ParametricSurfaces is also available.
Pre-made CSG Shapes
There are also some shortcut methods available to create common CSG objects more easily:
OpticSim.BoundedCylinder — FunctionBoundedCylinder(radius::T, height::T; interface::NullOrFresnel{T} = nullinterface(T)) -> CSGGenerator{T}Create a cylinder with planar caps on both ends centred at (0, 0, 0) with axis (0, 0, 1).
OpticSim.Cuboid — FunctionCuboid(halfsizex::T, halfsizey::T, halfsizez::T; interface::NullOrFresnel{T} = nullinterface(T)) -> CSGGenerator{T}Create a cuboid centred at (0, 0, 0).
OpticSim.HexagonalPrism — FunctionHexagonalPrism(side_length::T, visheight::T = 2.0; interface::NullOrFresnel{T} = nullinterface(T)) -> CSGGenerator{T}Create an infinitely tall hexagonal prism with axis (0, 0, 1), the longer hexagon diameter is along the x axis. For visualization visheight is used, note that this does not fully represent the surface.
OpticSim.RectangularPrism — FunctionRectangularPrism(halfsizex::T, halfsizey::T, visheight::T=2.0; interface::NullOrFresnel{T} = nullinterface(T)) -> CSGGenerator{T}Create an infinitely tall rectangular prism with axis (0, 0, 1). For visualization visheight is used, note that this does not fully represent the surface.
OpticSim.TriangularPrism — FunctionTriangularPrism(side_length::T, visheight::T = 2.0; interface::NullOrFresnel{T} = nullinterface(T)) -> CSGGenerator{T}Create an infinitely tall triangular prism with axis (0, 0, 1). For visualization visheight is used, note that this does not fully represent the surface.
OpticSim.Spider — FunctionSpider(narms::Int, armwidth::T, radius::T, origin::SVector{3,T} = SVector{3,T}(0.0, 0.0, 0.0), normal::SVector{3,T} = SVector{3,T}(0.0, 0.0, 1.0)) -> Vector{Rectangle{T}}Creates a 'spider' obscuration with narms rectangular arms evenly spaced around a circle defined by origin and normal. Each arm is a rectangle armwidth×radius.
e.g. for 3 and 4 arms we get:
| _|_
/ \ |Transforms
Transforms are used to position does within the CSG tree.
OpticSim.RigidBodyTransform — TypeRigidBodyTransform{S<:Real}Transform encapsulating rotation and translation in 3D space. Translation happens after rotation.
RigidBodyTransform{S}(θ::T, ϕ::T, ψ::T, x::T, y::T, z::T)
RigidBodyTransform(rotation::SMatrix{3,3,S}, translation::SVector{3,S})
RigidBodyTransform(rotation::AbstractArray{S,2}, translation::AbstractArray{S,1})θ, ϕ and ψ in first constructor are in radians.
OpticSim.rotation — Functionrotation([S::Type], θ::T, ϕ::T, ψ::T) -> RigidBodyTransform{S}Returns the RigidBodyTransform of type S (default Float64) representing the rotation by θ, ϕ and ψ around the x, y and z axes respectively in radians.
OpticSim.rotationd — Functionrotationd([S::Type], θ::T, ϕ::T, ψ::T) -> RigidBodyTransform{S}Returns the RigidBodyTransform of type S (default Float64) representing the rotation by θ, ϕ and ψ around the x, y and z axes respectively in degrees.
OpticSim.translation — Functiontranslation([S::Type], x::T, y::T, z::T) -> RigidBodyTransform{S}Returns the RigidBodyTransform of type S (default Float64) representing the translation by x, y and z.
OpticSim.rotmat — Functionrotmat([S::Type], θ::T, ϕ::T, ψ::T) -> SMatrix{3,3,S}Returns the rotation matrix of type S (default Float64) representing the rotation by θ, ϕ and ψ around the x, y and z axes respectively in radians.
OpticSim.rotmatd — Functionrotmatd([S::Type], θ::T, ϕ::T, ψ::T) -> SMatrix{3,3,S}Returns the rotation matrix of type S (default Float64) representing the rotation by θ, ϕ and ψ around the x, y and z axes respectively in degrees.
OpticSim.rotmatbetween — Functionrotmatbetween([S::Type], a::SVector{3,T}, b::SVector{3,T}) -> SMatrix{3,3,S}Returns the rotation matrix of type S (default Float64) representing the rotation between vetors a and b.
CSG Types
These are the types of the primary CSG elements, i.e. the nodes in the CSG tree.
OpticSim.CSGTree — TypeAbstract type representing any evaluated CSG structure.
OpticSim.CSGGenerator — TypeCSGGenerator{T<:Real}This is the type you should use when making CSG objects. This type allows for the construction of CSGTree objects with different transforms. When the generator is evaluated, all transforms are propagated down to the LeafNodes and stored there.
Example
a = Cylinder(1.0,1.0)
b = Plane([0.0,0.0,1.0], [0.0,0.0,0.0])
generator = csgintersection(a,b)
# now make a csg object that can be ray traced
csgobj = generator(RigidBodyTransform(1.0,1.0,2.0))OpticSim.ComplementNode — TypeComplementNode{T,C<:CSGTree{T}} <: CSGTree{T}An evaluated complement node within the CSG tree, must be the second child of a IntersectionNode forming a subtraction.
OpticSim.UnionNode — TypeUnionNode{T,L<:CSGTree{T},R<:CSGTree{T}} <: CSGTree{T}An evaluated union node within the CSG tree.
OpticSim.IntersectionNode — TypeIntersectionNode{T,L<:CSGTree{T},R<:CSGTree{T}} <: CSGTree{T}An evaluated intersection node within the CSG tree.
OpticSim.LeafNode — TypeLeafNode{T,S<:ParametricSurface{T}} <: CSGTree{T}An evaluated leaf node in the CSG tree, geometry attribute which contains a ParametricSurface of type S. The leaf node also has a transform associated which is the composition of all nodes above it in the tree. As such, transforming points from the geometry using this transform puts them in world space, and transforming rays by the inverse transform puts them in object space.
Additional Functions and Types
These are the internal types and functions used for geomertic/CSG operations.
Functions
OpticSim.surfaceintersection — Methodsurfaceintersection(obj::CSGTree{T}, r::AbstractRay{T,N})Calculates the intersection of r with CSG object, obj.
Returns an EmptyInterval if there is no intersection, an Interval if there is one or two interesections and a DisjointUnion if there are more than two intersections.
The ray is intersected with the LeafNodes that make up the CSG object and the resulting Intervals and DisjointUnions are composed with the same boolean operations to give a final result. The ray is transformed by the inverse of the transform associated with the leaf node to put it in object space for that node before the intersection is carried out, typically this object space is centered at the origin, but may differ for each primitive.
Some intersections are culled without actually evaluating them by first checking if the ray intersects the BoundingBox of each node in the CSGTree, this can substantially improve performance in some cases.
OpticSim.inside — Methodinside(obj::CSGTree{T}, point::SVector{3,T}) -> Bool
inside(obj::CSGTree{T}, x::T, y::T, z::T) -> BoolTests whether a 3D point in world space is inside obj.
OpticSim.onsurface — Methodonsurface(obj::CSGTree{T}, point::SVector{3,T}) -> Bool
onsurface(obj::CSGTree{T}, x::T, y::T, z::T) -> BoolTests whether a 3D point in world space is on the surface (i.e. shell) of obj.
Intervals
OpticSim.Interval — TypeInterval{T} <: AbstractRayInterval{T}Datatype representing an interval between two IntervalPoints on a ray.
The lower element can either be RayOrigin or an Intersection. The upper element can either be an Intersection or Infinity.
positivehalfspace(int::Intersection) -> Interval with lower = int, upper = Infinity
rayorigininterval(int::Intersection) -> Interval with lower = RayOrigin, upper = int
Interval(low, high)Has the following accessor methods:
lower(a::Interval{T}) -> Union{RayOrigin{T},Intersection{T,3}}
upper(a::Interval{T}) -> Union{Intersection{T,3},Infinity{T}}OpticSim.EmptyInterval — TypeEmptyInterval{T} <: AbstractRayInterval{T}An interval with no Intersections which is also not infinite.
EmptyInterval(T = Float64)
EmptyInterval{T}()OpticSim.DisjointUnion — TypeDatatype representing an ordered series of disjoint intervals on a ray. An arbitrary array of Intervals can be input to the constructor and they will automatically be processed into a valid DisjointUnion (or a single Interval if appropriate).
DisjointUnion(intervals::AbstractVector{Interval{R}})OpticSim.isemptyinterval — Functionisemptyinterval(a) -> BoolReturns true if a is an EmptyInterval. In performance critical contexts use a isa EmptyInterval{T}.
OpticSim.ispositivehalfspace — Functionispositivehalfspace(a) -> BoolReturns true if upper(a) is Infinity. In performance critical contexts check directly i.e. upper(a) isa Infinity{T}.
OpticSim.israyorigininterval — Functionisrayorigininterval(a) -> BoolReturns true if lower(a) is RayOrigin. In performance critical contexts check directly i.e. lower(a) isa RayOrigin{T}.
OpticSim.halfspaceintersection — Functionhalfspaceintersection(a::Interval{T}) -> Intersection{T,3}Returns the Intersection from a half space Interval, throws an error if not a half space.
OpticSim.closestintersection — Functionclosestintersection(a::Union{EmptyInterval{T},Interval{T},DisjointUnion{T}}, ignorenull::Bool = true) -> Union{Nothing,Intersection{T,3}}Returns the closest Intersection from an Interval or DisjointUnion. Ignores intersection with null interfaces if ignorenull is true. Will return nothing if there is no valid intersection.
OpticSim.IntervalPool — TypeTo prevent allocations we have a manually managed pool of arrays of Intervals which are used to store values during execution. The memory is kept allocated and reused across runs of functions like trace.
threadedintervalpool is a global threadsafe pool which is accessed through the functions:
newinintervalpool!(::Type{T} = Float64, tid::Int = Threads.threadid()) -> Vector{Interval{T}}
indexednewinintervalpool!(::Type{T} = Float64, tid::Int = Threads.threadid()) -> Tuple{Int,Vector{Interval{T}}}
emptyintervalpool!(::Type{T} = Float64, tid::Int = Threads.threadid())
getfromintervalpool([::Type{T} = Float64], id::Int, tid::Int = Threads.threadid()) -> Vector{Interval{T}}Intersections
OpticSim.IntervalPoint — TypeEach Interval consists of two IntervalPoints, one of RayOrigin, Intersection or Infinity.
OpticSim.RayOrigin — TypeRayOrigin{T} <: IntervalPoint{T}Point representing 0 within an Interval, i.e. the start of the ray.
RayOrigin(T = Float64)
RayOrigin{T}()OpticSim.Infinity — TypeInfinity{T} <: IntervalPoint{T}Point representing ∞ within an Interval.
Infinity(T = Float64)
Infinity{T}()OpticSim.Intersection — TypeIntersection{T,N} <: IntervalPoint{T}Represents the point at which an Ray hits a Surface. This consists of the distance along the ray, the intersection point in world space, the normal in world space, the UV on the surface and the OpticalInterface hit.
Has the following accessor methods:
point(a::Intersection{T,N}) -> SVector{N,T}
normal(a::Intersection{T,N}) -> SVector{N,T}
uv(a::Intersection{T,N}) -> SVector{2,T}
u(a::Intersection{T,N}) -> T
v(a::Intersection{T,N}) -> T
α(a::Intersection{T,N}) -> T
interface(a::Intersection{T,N}) -> OpticalInterface{T}
flippednormal(a::Intersection{T,N}) -> BoolOpticSim.isinfinity — Functionisinfinity(a) -> BoolReturns true if a is Infinity. In performance critical contexts use a isa Infinity{T}.
OpticSim.israyorigin — Functionisrayorigin(a) -> BoolReturns true if a is RayOrigin. In performance critical contexts use a isa RayOrigin{T}.