ToRA:
A Tool-Integrated Reasoning Agent
for Mathematical Problem Solving

Zhibin Gou^1,2*, Zhihong Shao^1,2*, Yeyun Gong^2†, Yelong Shen²
Yujiu Yang^1†, Minlie Huang^1†, Nan Duan², Weizhu Chen²

¹Tsinghua University, ²Microsoft
ICLR 2024
^*Equal Contribution ^†Corresponding Authors

Figure 1: Comparing ToRA with baselines on LLaMA-2 base models from 7B to 70B.

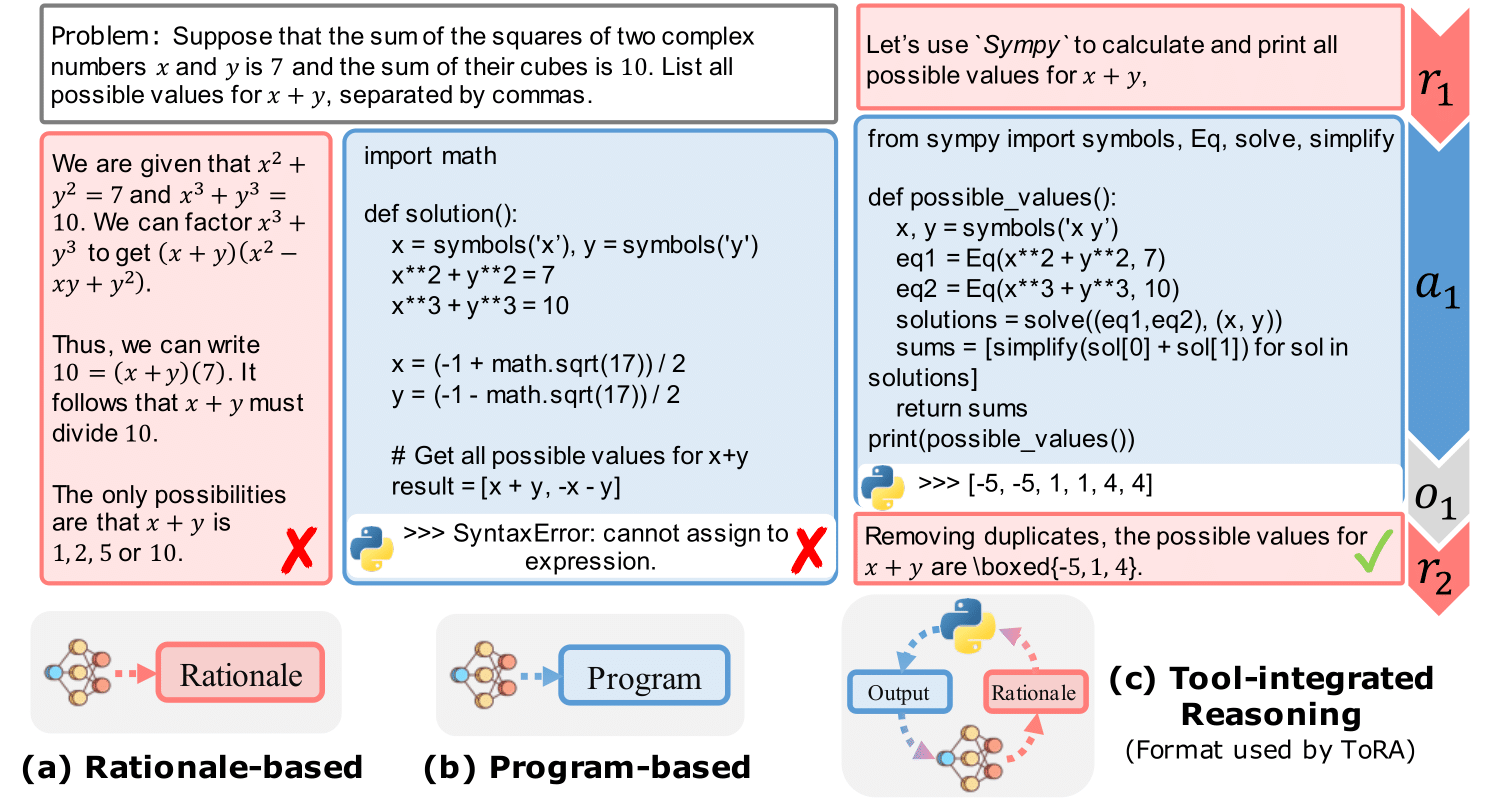
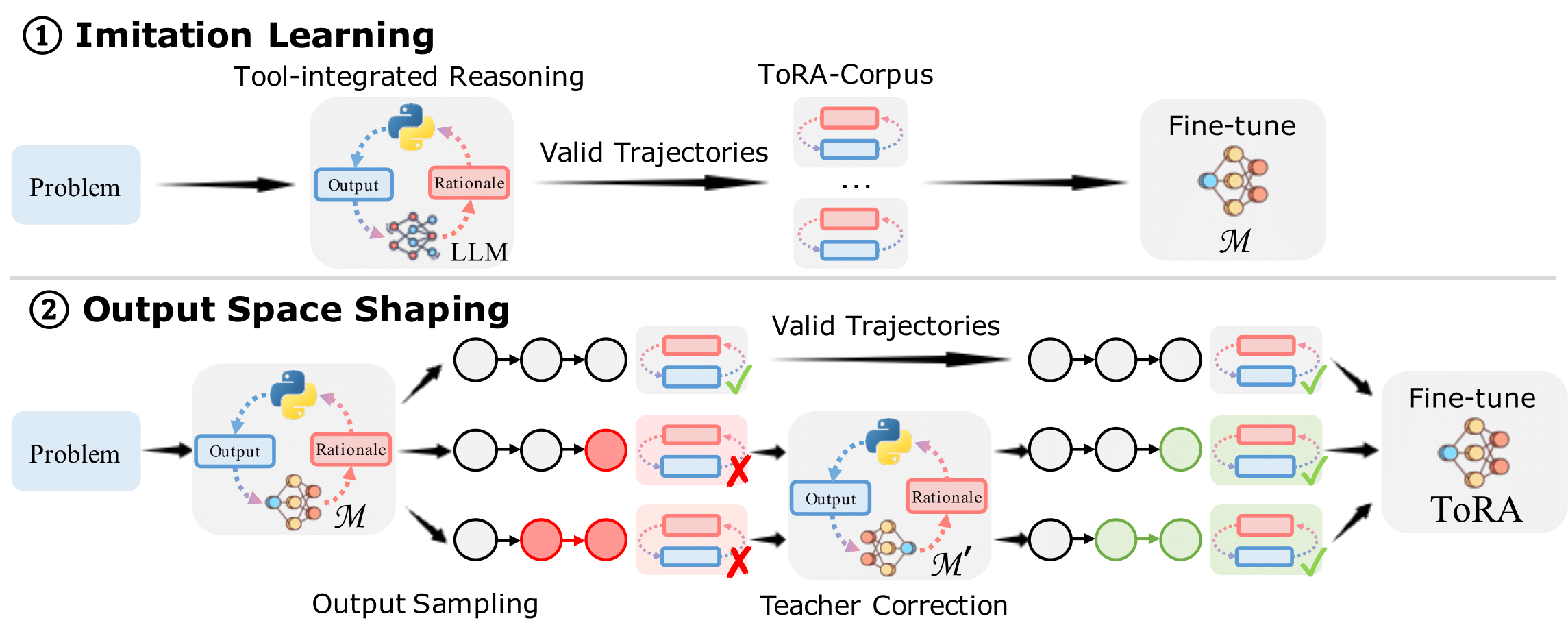
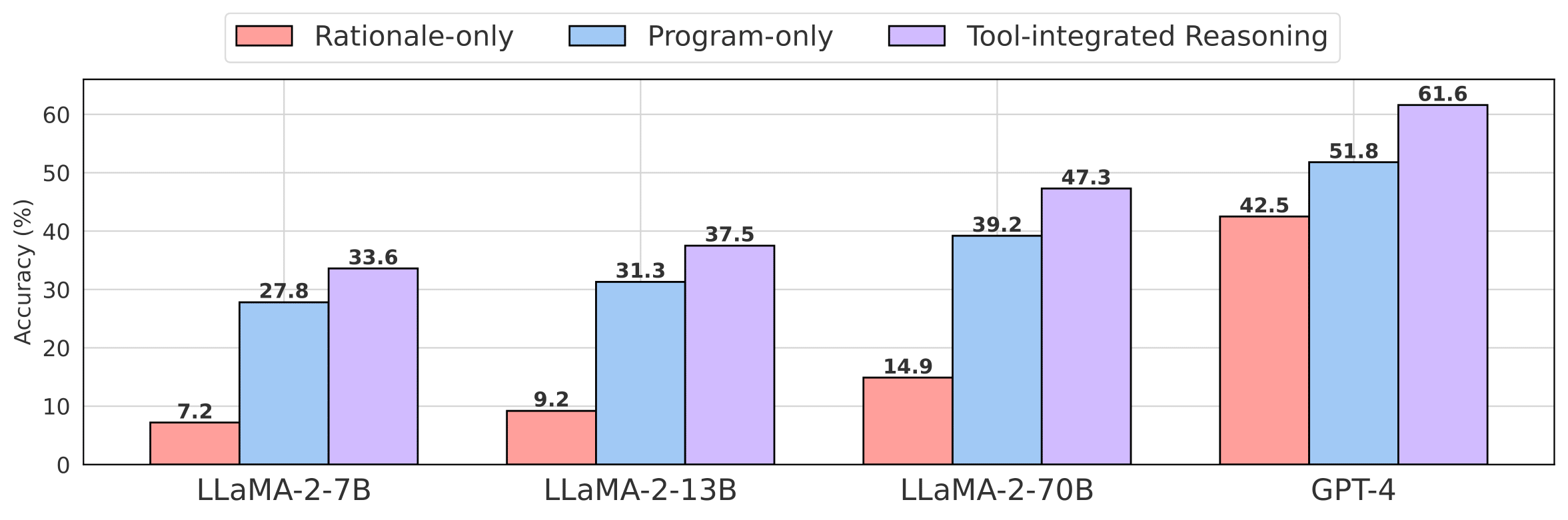
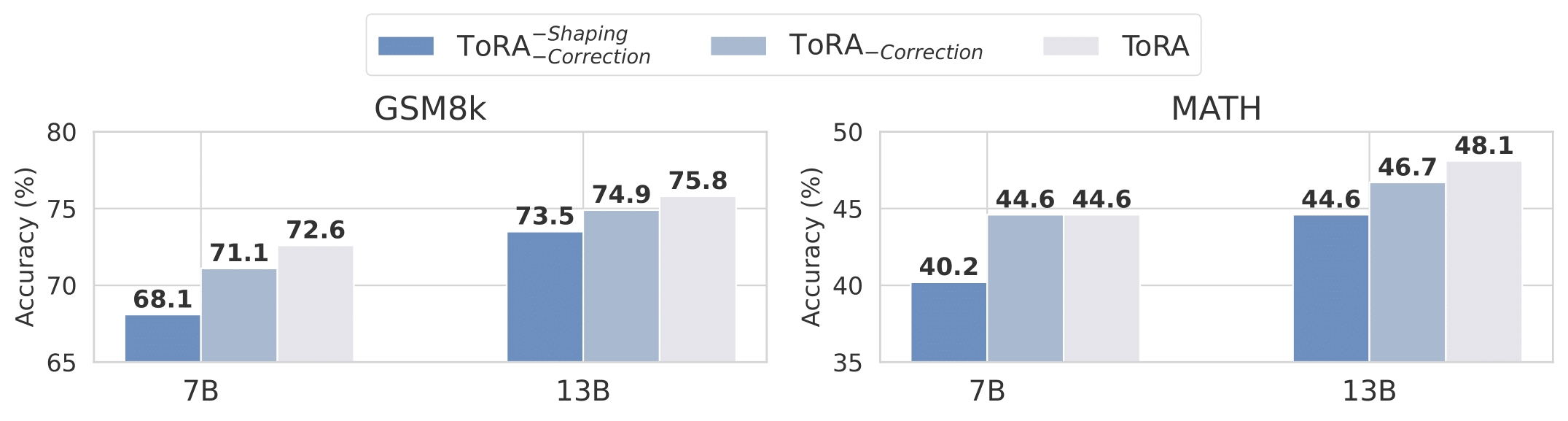
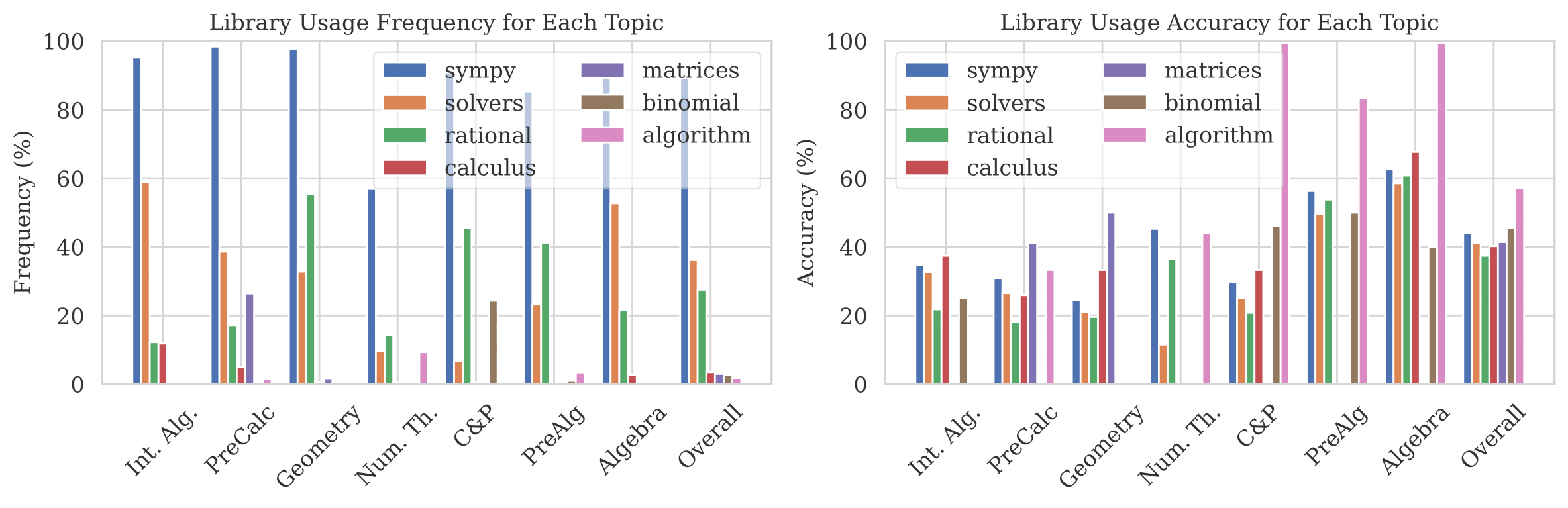
ToRA is a series of Tool-integrated Reasoning Agents designed to solve challenging mathematical reasoning problems by interacting with tools, e.g., computation libraries and symbolic solvers. ToRA series seamlessly integrate natural language reasoning with the utilization of external tools, thereby amalgamating the analytical prowess of language and the computational efficiency of external tools.

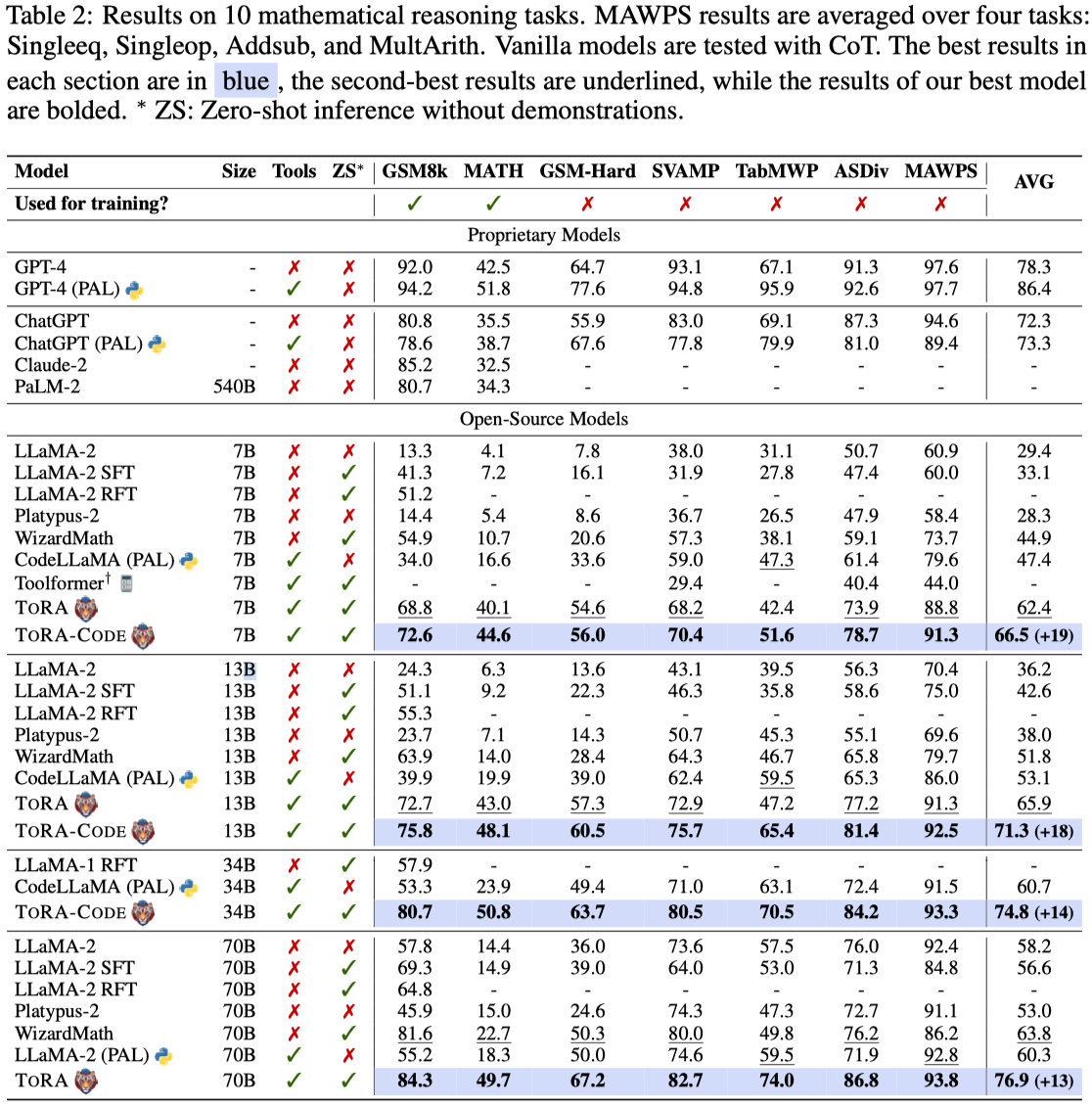
ToRA models significantly outperform open-source models on 10 mathematical reasoning datasets across all scales with 13%-19% absolute improvements on average. Notably, ToRA-7B reaches 44.6% on the competition-level dataset MATH, surpassing the best open-source model WizardMath-70B by 22% absolute. ToRA-Code-34B is also the first open-source model that achieves an accuracy exceeding 50% on MATH, which significantly outperforms GPT-4’s CoT result, and is competitive with GPT-4 solving problems with programs.

Tool-Integrated Reasoning

Figure 2: A basic example of single-round tool interaction that interleaves rationales with program-based tool use.

ToRA adopts a tool-integrated reasoning format that interweaves natural language reasoning with program-based tool use (Figure 2). This format effectively combines the advantages of semantic analysis, planning, and abstract reasoning in language reasoning with the precise calculation, symbolic operation, and efficient algorithm execution of tool use, thereby effectively addressing the challenges of complex mathematical reasoning tasks.

Table 1: Compared with mathematical reasoning datasets, ToRA-Corpus uniquely combines natural language rationales with program-based tool usage. Note that ToRA-Corpus only employ questions from the original training set of MATH and GSM8k.

Based on the interleaving format of tool-integrated reasoning, we use GPT-4 to collect high-quality interactive tool-use trajectories for mathematical problems in the GSM8k and MATH datasets, forming a ToRA-Corpus with only 16k annotations. We apply imitation learning for fine-tuning on this dataset, and find that the fine-tuned imitation models can achieve SoTA performance.

Output Space Shaping

Figure 3: Training TORA contains two steps. ① Imitation Learning: Prompt LLMs like GPT-4 to generate Tool-integrated Reasoning trajectories (ToRA-Corpus) and use this corpus to fine-tune a model M; ② Output Space Shaping: Sample diverse tool-use trajectories with M, keep the valid ones, correct the invalid ones with a teacher model M′, and retrain M on the union of sampled valid trajectories, corrected ones, and the initial ToRA-Corpus to obtain ToRA.

Furthermore, to increase the diversity of reasoning steps and reduce improper tool-use behavior, we propose an output space shaping method (Figure 3): using imitation model M to perform diverse self-sampling of tool-use trajectories, retaining valid trajectories, correcting invalid trajectories with teacher model M', and fine-tuning model M on valid trajectories, corrected trajectories, and initial imitation trajectories ToRA-Corpus to obtain the final ToRA model. This method significantly improves reasoning performance, enabling open-source models to achieve over 50% accuracy on the competition-level MATH dataset for the first time.

Experiments

The above figure shows the results of ToRA on 10 diverse mathematical reasoning datasets. We can find that:

ToRA consistently outperforms state-of-the-art open-source models, achieving significant improvements of 13%-19% on average across 10 tasks. ToRA-70B significantly outperforms ChatGPT on GSM8k (84.3% vs. 80.4%) and MATH (49.7% vs. 38.7%), while ToRA-Code-34B greatly surpasses GPT-4 CoT on competition-level MATH dataset (50.8% vs. 42.5%), and is comparable to GPT-4 PAL using code to solve problems (50.8% vs. 51.8%).
Based on CodeLLaMA training, ToRA-Code's accuracy is about 5% higher than that of ToRA based on LLaMA-2 with the same parameter size, indicating that improving the base model's code capability can further enhance ToRA's problem-solving ability.
ToRA exhibits superior generalization ability, while CoT fine-tuning based on language rationales may have negative effects on OOD generalization. For example, ToRA-70B generalizes better on TabMWP, a table reasoning task, than WizardMath (74.0% vs. 57.5%).
ToRA achieves fast zero-shot inference, averaging 1.02 tool interaction rounds per problem, maintaining high efficiency with one round of interaction for most problems.

Figure 4: Comparison of three formats: (1) Rationale-only: step-by-step natural language reasoning like CoT; (2) Program-only: solving problems with programs like PAL; (3) Tool-integrated Reasoning used by TORA: interweaving rationale and program execution to solve problems. We train LLaMA-2 models to reason in the three types of formats. We evaluated GPT-4 with few-shot prompting.

Figure 4 shows that compared to using only language reasoning (Rationale-only) or only program-based tool use (Program-only), Tool-integrated Reasoning has better performance in mathematical reasoning tasks.

Figure 5: Ablation on output space shaping strategies using CodeLLaMA.

By conducting ablation on the proposed output space shaping strategies (Figure 5), we demonstrate that output space shaping plays a crucial role in enhancing the ability to solve mathematical problems.

Analysis

Figure 6: Library usage frequency and accuracy on each sub-topic of MATH.

In addition, we analyze the benefits and remaining challenges of tool interaction for mathematical reasoning, providing valuable insights for future work. Please refer to our paper for details.

BibTeX

@misc{gou2023tora,
    title={ToRA: A Tool-Integrated Reasoning Agent for Mathematical Problem Solving}, 
    author={Zhibin Gou and Zhihong Shao and Yeyun Gong and yelong shen and Yujiu Yang and Minlie Huang and Nan Duan and Weizhu Chen},
    year={2023},
    eprint={2309.17452},
    archivePrefix={arXiv},
    primaryClass={cs.CL}
}