10.3 实现逻辑异或门
10.3 实现逻辑异或门⚓︎
10.3.1 代码实现⚓︎
准备数据⚓︎
异或数据比较简单,只有4个记录,所以就hardcode在此,不用再建立数据集了。这也给读者一个机会了解如何从DataReader类派生出一个全新的子类XOR_DataReader。
比如在下面的代码中,我们覆盖了父类中的三个方法:
init()初始化方法:因为父类的初始化方法要求有两个参数,代表train/test数据文件ReadData()方法:父类方法是直接读取数据文件,此处直接在内存中生成样本数据,并且直接令训练集等于原始数据集(不需要归一化),令测试集等于训练集GenerateValidationSet()方法,由于只有4个样本,所以直接令验证集等于训练集
因为NeuralNet2中的代码要求数据集比较全,有训练集、验证集、测试集,为了已有代码能顺利跑通,我们把验证集、测试集都设置成与训练集一致,对于解决这个异或问题没有什么影响。
class XOR_DataReader(DataReader):
def ReadData(self):
self.XTrainRaw = np.array([0,0,0,1,1,0,1,1]).reshape(4,2)
self.YTrainRaw = np.array([0,1,1,0]).reshape(4,1)
self.XTrain = self.XTrainRaw
self.YTrain = self.YTrainRaw
self.num_category = 1
self.num_train = self.XTrainRaw.shape[0]
self.num_feature = self.XTrainRaw.shape[1]
self.XTestRaw = self.XTrainRaw
self.YTestRaw = self.YTrainRaw
self.XTest = self.XTestRaw
self.YTest = self.YTestRaw
self.num_test = self.num_train
def GenerateValidationSet(self, k = 10):
self.XVld = self.XTrain
self.YVld = self.YTrain
测试函数⚓︎
与第6章中的逻辑与门和或门一样,我们需要神经网络的运算结果达到一定的精度,也就是非常的接近0,1两端,而不是说勉强大于0.5就近似为1了,所以精度要求是误差绝对值小于1e-2。
def Test(dataReader, net):
print("testing...")
X,Y = dataReader.GetTestSet()
A = net.inference(X)
diff = np.abs(A-Y)
result = np.where(diff < 1e-2, True, False)
if result.sum() == dataReader.num_test:
return True
else:
return False
主过程代码⚓︎
if __name__ == '__main__':
......
n_input = dataReader.num_feature
n_hidden = 2
n_output = 1
eta, batch_size, max_epoch = 0.1, 1, 10000
eps = 0.005
hp = HyperParameters2(n_input, n_hidden, n_output, eta, max_epoch, batch_size, eps, NetType.BinaryClassifier, InitialMethod.Xavier)
net = NeuralNet2(hp, "Xor_221")
net.train(dataReader, 100, True)
......
此处的代码有几个需要强调的细节:
n_input = dataReader.num_feature,值为2,而且必须为2,因为只有两个特征值n_hidden=2,这是人为设置的隐层神经元数量,可以是大于2的任何整数eps精度=0.005是后验知识,笔者通过测试得到的停止条件,用于方便案例讲解- 网络类型是
NetType.BinaryClassifier,指明是二分类网络 - 最后要调用
Test函数验证精度
10.3.2 运行结果⚓︎
经过快速的迭代后,会显示训练过程如图10-10所示。
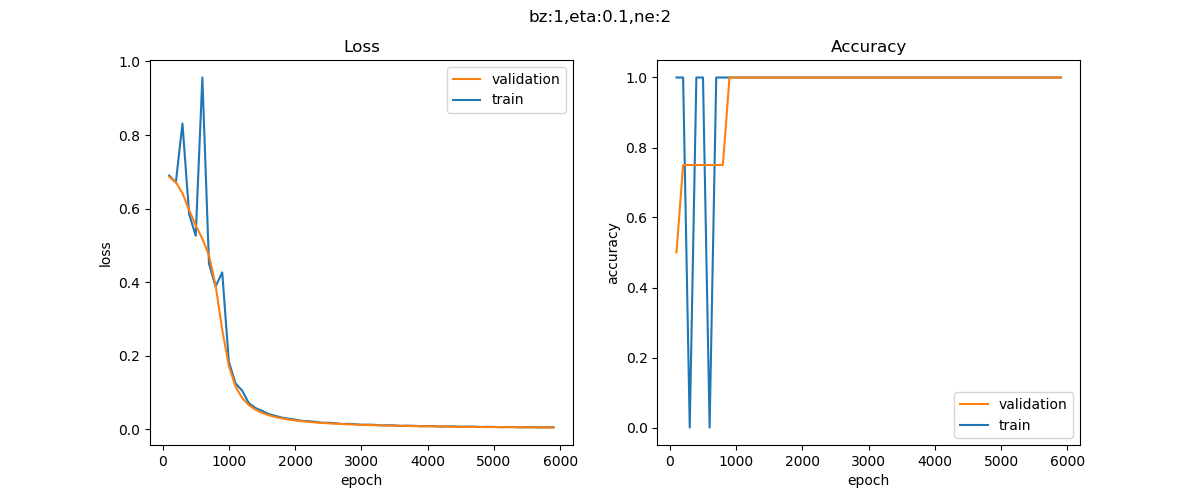
图10-10 训练过程中的损失函数值和准确率值的变化
可以看到二者的走势很理想。
同时在控制台会打印一些信息,最后几行如下:
......
epoch=5799, total_iteration=23199
loss_train=0.005553, accuracy_train=1.000000
loss_valid=0.005058, accuracy_valid=1.000000
epoch=5899, total_iteration=23599
loss_train=0.005438, accuracy_train=1.000000
loss_valid=0.004952, accuracy_valid=1.000000
W= [[-7.10166559 5.48008579]
[-7.10286572 5.48050039]]
B= [[ 2.91305831 -8.48569781]]
W= [[-12.06031599]
[-12.26898815]]
B= [[5.97067802]]
testing...
1.0
None
testing...
A2= [[0.00418973]
[0.99457721]
[0.99457729]
[0.00474491]]
True
epoch,达到了指定的loss精度(0.005),loss_valid是0.004991,刚好小于0.005时停止迭代。
我们特意打印出了A2值,即网络推理结果,如表10-7所示。
表10-7 异或计算值与神经网络推理值的比较
| x1 | x2 | XOR | Inference | diff |
|---|---|---|---|---|
| 0 | 0 | 0 | 0.0041 | 0.0041 |
| 0 | 1 | 1 | 0.9945 | 0.0055 |
| 1 | 0 | 1 | 0.9945 | 0.0055 |
| 1 | 1 | 0 | 0.0047 | 0.0047 |
表中第四列的推理值与第三列的XOR结果非常的接近,继续训练的话还可以得到更高的精度,但是一般没这个必要了。由此我们再一次认识到,神经网络只可以得到无限接近真实值的近似解。
代码位置⚓︎
ch10, Level1