15.4 算法效果比较
15.4 算法在等高线图上的效果比较⚓︎
15.4.1 模拟效果比较⚓︎
为了简化起见,我们先用一个简单的二元二次函数来模拟损失函数的等高线图,测试一下我们在前面实现的各种优化器。但是以下测试结果只是一个示意性质的,可以理解为在绝对理想的条件下(样本无噪音,损失函数平滑等等)的各算法的表现。
z = \frac{x^2}{10} + y^2 \tag{1}
公式1是模拟均方差函数的形式,它的正向计算和反向计算的Python代码如下:
def f(x, y):
return x**2 / 10.0 + y**2
def derivative_f(x, y):
return x / 5.0, 2.0*y
我们依次测试4种方法:
- 普通SGD, 学习率0.95
- 动量Momentum, 学习率0.1
- RMPSProp,学习率0.5
- Adam,学习率0.5
每种方法都迭代20次,记录下每次反向过程的(x,y)坐标点,绘制图15-8如下。
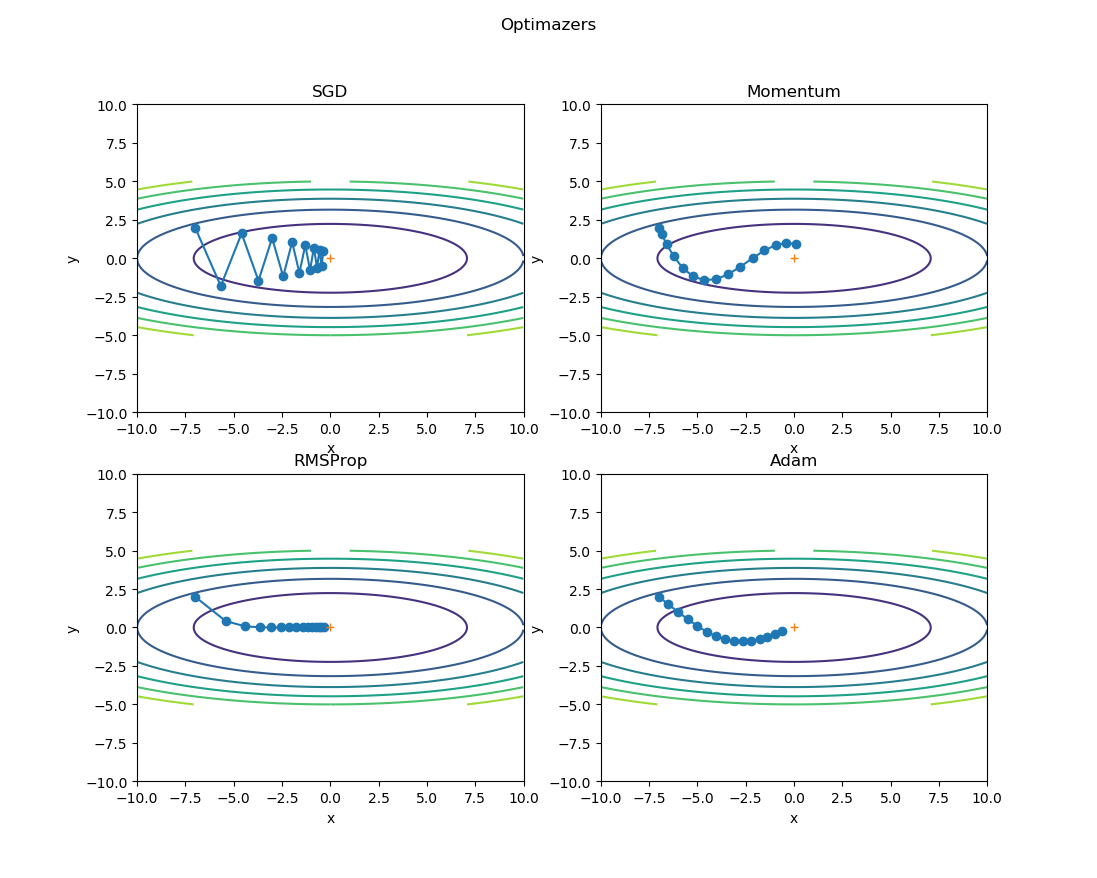
图15-8 不同梯度下降优化算法的模拟比较
- SGD算法,每次迭代完全受当前梯度的控制,所以会以折线方式前进。
- Momentum算法,学习率只有0.1,每次继承上一次的动量方向,所以会以比较平滑的曲线方式前进,不会出现突然的转向。
- RMSProp算法,有历史梯度值参与做指数加权平均,所以可以看到比较平缓,不会波动太大,都后期步长越来越短也是符合学习规律的。
- Adam算法,因为可以被理解为Momentum和RMSProp的组合,所以比Momentum要平缓一些,比RMSProp要平滑一些。
15.4.2 真实效果比较⚓︎
下面我们用第四章线性回归的例子来做实际的测试。为什么要用线性回归的例子呢?因为在它只有w, b两个变量需要求解,可以在二维平面或三维空间来表现,这样我们就可以用可视化的方式来解释算法的效果。
下面列出了用Python代码实现的前向计算、反向计算、损失函数计算的函数:
def ForwardCalculationBatch(W,B,batch_x):
Z = np.dot(W, batch_x) + B
return Z
def BackPropagationBatch(batch_x, batch_y, batch_z):
m = batch_x.shape[1]
dZ = batch_z - batch_y
dB = dZ.sum(axis=1, keepdims=True)/m
dW = np.dot(dZ, batch_x.T)/m
return dW, dB
def CheckLoss(W, B, X, Y):
m = X.shape[1]
Z = np.dot(W, X) + B
LOSS = (Z - Y)**2
loss = LOSS.sum()/m/2
return loss
损失函数用的是均方差,回忆一下公式:
J(w,b) = \frac{1}{2}(Z-Y)^2 \tag{2}
如果把公式2展开的话:
J = \frac{1}{2} (Z^2 + Y^2 - 2ZY)
其形式比公式1多了最后一项,所以画出来的损失函数的等高线是斜向的椭圆。下面是画等高线的代码方法,详情请移步代码库:
def show_contour(ax, loss_history, optimizer):
这里有个matplotlib的绘图知识:
- 确定
x_axis值的范围:w = np.arange(1,3,0.01),因为w的准确值是2 - 确定
y_axis值的范围:b = np.arange(2,4,0.01),因为b的准确值是3 - 生成网格数据:
W,B = np.meshgrid(w, b) - 计算每个网点上的损失函数值Z
- 所以(W,B,Z)形成了一个3D图,最后用
ax.coutour(W,B,Z)来绘图 levels参数是控制等高线的精度或密度,norm控制颜色的非线性变化
表15-10 各种算法的效果比较
 |
 |
| SGD当学习率为0.1时,需要很多次迭代才能逐渐向中心靠近 | SGD当学习率为0.5时,会比较快速地向中心靠近,但是在中心的附近有较大震荡 |
 |
 |
| Momentum由于惯性存在,一下子越过了中心点,但是很快就会得到纠正 | Nag是Momentum的改进,有预判方向功能 |
 |
 |
| AdaGrad的学习率在开始时可以设置大一些,因为会很快衰减 | AdaDelta即使把学习率设置为0,也不会影响,因为有内置的学习率策略 |
 |
 |
| RMSProp解决AdaGrad的学习率下降问题,即使学习率设置为0.1,收敛也会快 | Adam到达中点的路径比较直接 |
在表15-10中,观察其中4组优化器的训练轨迹:
- SGD:在较远的地方,沿梯度方向下降,越靠近中心的地方,抖动得越多,似乎找不准方向,得到loss值等于0.005迭代了148次。
- Momentum:由于惯性存在,一下子越过了中心点,但是很快就会得到纠正,得到loss值等于0.005迭代了128次。
- RMSProp:与SGD的行为差不多,抖动大,得到loss值等于0.005迭代了130次。
- Adam:与Momentum一样,越过中心点,但后来的收敛很快,得到loss值等于0.005迭代了107次。
为了能看清最后几步的行为,我们放大每张图,如图15-9所示,再看一下。
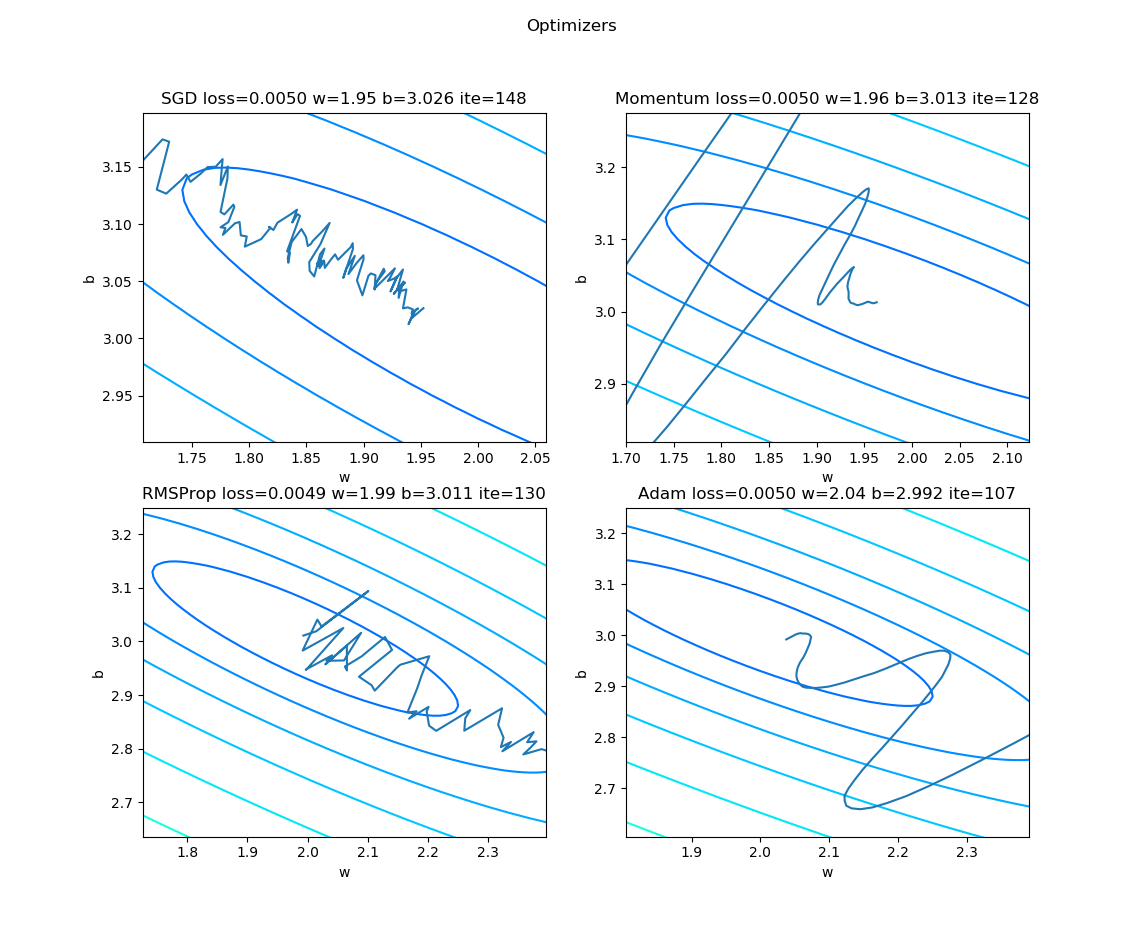
图15-9 放大后各优化器的训练轨迹
- SGD:接近中点的过程很曲折,步伐很慢,甚至有反方向的,容易陷入局部最优。
- Momentum:快速接近中点,但中间跳跃较大。
- RMSProp:接近中点很曲折,但是没有反方向的,用的步数比SGD少,跳动较大,有可能摆脱局部最优解的。
- Adam:快速接近中点,难怪很多人喜欢用这个优化器。
代码位置⚓︎
ch15, Level4