17.2 卷积前向计算代码实现
17.2 卷积前向计算代码实现⚓︎
17.2.1 卷积核的实现⚓︎
卷积核,实际上和全连接层一样,是权重矩阵加偏移向量的组合,区别在于全连接层中的权重矩阵是二维的,偏移矩阵是列向量,而卷积核的权重矩阵是四维的,偏移矩阵是也是列向量。
class ConvWeightsBias(WeightsBias_2_1):
def __init__(self, output_c, input_c, filter_h, filter_w, init_method, optimizer_name, eta):
self.FilterCount = output_c
self.KernalCount = input_c
self.KernalHeight = filter_h
self.KernalWidth = filter_w
...
def Initialize(self, folder, name, create_new):
self.WBShape = (self.FilterCount, self.KernalCount, self.KernalHeight, self.KernalWidth)
...
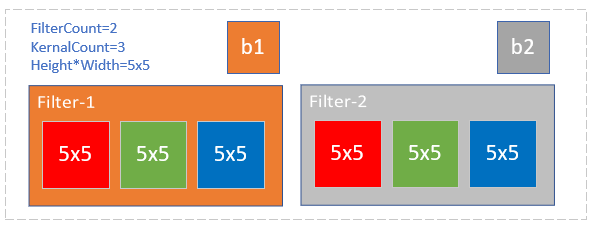
图17-19 卷积核的组成
以图17-19为例,各个维度的数值如下:
- FilterCount=2,第一维,过滤器数量,对应输出通道数。
- KernalCount=3,第二维,卷积核数量,对应输入通道数。两个Filter里面的Kernal数必须相同。
- KernalHeight=5,KernalWidth=5,卷积核的尺寸,第三维和第四维。同一组WeightsBias里的卷积核尺寸必须相同。
在初始化函数中,会根据四个参数定义WBShape,然后在CreateNew函数中,创建相应形状的Weights和Bias。
17.2.2 卷积前向运算的实现 - 方法1⚓︎
class ConvLayer(CLayer):
def forward(self, x, train=True):
self.x = x
self.batch_size = self.x.shape[0]
# 如果有必要的话,先对输入矩阵做padding
if self.padding > 0:
self.padded = np.pad(...)
else:
self.padded = self.x
#end if
self.z = conv_4d(...)
return self.z
上述代码中的conv_4d()函数实现了17.1中定义的四维卷积运算:
def conv_4d(x, weights, bias, out_h, out_w, stride=1):
batch_size = x.shape[0]
input_channel = x.shape[1]
output_channel = weights.shape[0]
filter_height = weights.shape[2]
filter_width = weights.shape[3]
rs = np.zeros((batch_size, num_output_channel, out_h, out_w))
for bs in range(batch_size):
for oc in range(output_channel):
rs[bs,oc] += bias[oc]
for ic in range(input_channel):
for i in range(out_h):
for j in range(out_w):
ii = i * stride
jj = j * stride
for fh in range(filter_height):
for fw in range(filter_width):
rs[bs,oc,i,j] += x[bs,ic,fh+ii,fw+jj] * weights[oc,ic,fh,fw]
上面的函数包含以下几重循环:
- 批量数据循环(第一维):
bs in batch_size,对每个样本进行计算; - 输出通道循环(第二维):
oc in output_channel。这里先把bias加上了,后加也可以; - 输入通道循环:
ic in input_channel; - 输出图像纵坐标循环:
i in out h; - 输出图像横坐标循环:
j in out_w。循环4和5完成对输出图像的每个点的遍历,在下面的子循环中计算并填充值; - 卷积核纵向循环(第三维):
fh in filter_height; - 卷积核横向循环(第四维):
fw in filter_width。循环6和7完成卷积核与输入图像的卷积计算,并保存到循环4和5指定的输出图像的点上。
我们试着运行上面的代码并循环10次,看看它的执行效率如何:
Time used for Python: 38.057225465774536
出乎我们的预料,在足足等了30多秒后,才返回结果。
通过试验发现,其运行速度非常慢,如果这样的函数在神经网络训练中被调用几十万次,其性能是非常糟糕的,这也是Python做为动态语言的一个缺点。
17.2.3 卷积前向运算的实现 - 方法2⚓︎
既然动态语言速度慢,我们把它编译成静态方法,是不是会快一些呢?
很幸运,有这样一个开源项目:numba,它可以在运行时把Python编译成C语言执行,代码是用C语言“风格”编写的Python代码,而且越像C的话,执行速度越快。
我们先用pip安装numba包:
pip install numba
然后在需要运行时编译的函数前面加上一个装饰符:
@nb.jit(nopython=True)
def jit_conv_4d(x, weights, bias, out_h, out_w, stride=1):
...
为了明确起见,我们把conv_4d前面加上一个jit前缀,表明这个函数是经过numba加速的。然后运行循环10次的测试代码:
Time used for Numba: 0.0727994441986084
又一次出乎我们的预料,这次只用了0.07秒,比纯Python代码快了500多倍!
但是不要急,我们还需要检查一下其正确性。方法1输出结果为output1,Numba编译后的方法输出结果为output2,二者都是四维矩阵,我们用np.allclose()函数来比较它们的差异:
print("correctness:", np.allclose(output1, output2, atol=1e-7))
得到的结果是:
correctness: True
np.allclose方法逐元素检查两种方法的返回值的差异,如果绝对误差在1e-7之内,说明两个返回的四维数组相似度极高,运算结果可信。
为什么不把所有的Python代码都编译成C代码呢?是因为numba的能力有限,并不支持numpy的所有函数,所以只能把关键的运算代码设计为独立的函数,然后用numba编译执行,函数的输入可以是数组、向量、标量,不能是复杂的自定义结构体或函数指针。
17.2.4 卷积前向运算的实现 - 方法3⚓︎
由于卷积操作是原始图片数据与卷积核逐点相乘的结果,所以遍历每个点的运算速度非常慢。在全连接层中,由于是两个矩阵直接相乘,所以速度非常快。我们是否可以把卷积操作转换为矩阵操作呢?
在Caffe框架中,巧妙地把逐点相乘的运算转换成了矩阵运算,大大提升了程序运行速度。这就是著名的im2col函数(我们在代码中命名为img2col)。
def forward_img2col(self, x, train=True):
self.x = x
self.batch_size = self.x.shape[0]
assert(self.x.shape == (self.batch_size, self.InC, self.InH, self.InW))
self.col_x = img2col(x, self.FH, self.FW, self.stride, self.padding)
self.col_w = self.WB.W.reshape(self.OutC, -1).T
self.col_b = self.WB.B.reshape(-1, self.OutC)
out1 = np.dot(self.col_x, self.col_w) + self.col_b
out2 = out1.reshape(batch_size, self.OutH, self.OutW, -1)
self.z = np.transpose(out2, axes=(0, 3, 1, 2))
return self.z
原理⚓︎
我们观察一下图17-20。
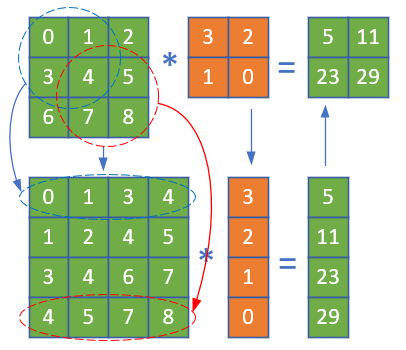
图17-20 把卷积运算转换成矩阵运算
先看上半部分:绿色的3\times 3矩阵为输入,经过棕色的卷积核运算后,得到右侧的2\times 2的矩阵。
再看图的下半部分:
第一步,上半部分中蓝色的虚线圆内的四个元素排列成第1行,形成[0,1,3,4],红色虚线圆内的四个元素排列成第4行[4,5,7,8],中间两行可以从右上角的[1,2,4,5]和左下角的[3,4,6,7]得到。这样,一个3\times 3的矩阵,就转换成了一个4\times 4的矩阵。也就是把卷积核视野中的每个二维2\times 2的数组变成1\times 4的向量。
第二步,把棕色的权重矩阵变成4\times 1的向量[3,2,1,0]。
第三步,把4\times 4的矩阵与4\times 1的向量相乘,得到4\times 1的结果向量[5,11,23,29]。
第四步:把4\times 1的结果变成2\times 2的矩阵,就得到了卷积运算的真实结果。
四维数组的展开⚓︎
前面只说明了二维数组的展开形式,四维数组可以用同样的方式展开。
我们假定有2个输入样本,每个样本含有3个通道,每个通道上是3\times 3的数据,则样本的原始形状和展开形状分别是:
x =
(样本1) [样本2]
(通道1) (通道1)
[[[[ 0 1 2] [[[27 28 29]
[ 3 4 5] [30 31 32]
[ 6 7 8]] [33 34 35]]
(通道2) (通道2)
[[ 9 10 11] [[36 37 38]
[12 13 14] [39 40 41]
[15 16 17]] [42 43 44]]
(通道3) (通道3)
[[18 19 20] [[45 46 47]
[21 22 23] [48 49 50]
[24 25 26]]] [51 52 53]]]]
------------------------------------------
col_x =
[[0. 1. 3. 4.| 9. 10. 12. 13.| 18. 19. 21. 22.]
[ 1. 2. 4. 5.| 10. 11. 13. 14.| 19. 20. 22. 23.]
[ 3. 4. 6. 7.| 12. 13. 15. 16.| 21. 22. 24. 25.]
[ 4. 5. 7. 8.| 13. 14. 16. 17.| 22. 23. 25. 26.]
----------------+----------------+----------------
[27. 28. 30. 31.| 36. 37. 39. 40.| 45. 46. 48. 49.]
[28. 29. 31. 32.| 37. 38. 40. 41.| 46. 47. 49. 50.]
[30. 31. 33. 34.| 39. 40. 42. 43.| 48. 49. 51. 52.]
[31. 32. 34. 35.| 40. 41. 43. 44.| 49. 50. 52. 53.]]
从生成的8\times 12的矩阵中可以观察到:
- 前4行是样本1的数据,后4行是样本2的数据
- 前4列是通道1的数据,中间4列是通道2的数据,后4列是通道3的数据
权重数组的展开⚓︎
对应的四维输入数据,卷积核权重数组也需要是四维的,其原始形状和展开后的形状如下:
weights=
(过滤器1) (过滤器2)
(卷积核1) (卷积核1)
[[[[ 0 1] [[[12 13]
[ 2 3]] [14 15]]
(卷积核2) (卷积核2)
[[ 4 5] [[16 17]
[ 6 7]] [18 19]]
(卷积核3) (卷积核3)
[[ 8 9] [[20 21]
[10 11]]] [22 23]]]]
---------------------------------------
col_w=
[[ 0 12]
[ 1 13]
[ 2 14]
[ 3 15]
[ 4 16]
[ 5 17]
[ 6 18]
[ 7 19]
[ 8 20]
[ 9 21]
[10 22]
[11 23]]
至此,展开数组已经可以和权重数组做矩阵相乘了。
结果数据的处理⚓︎
原始数据展开成了8\times 12的矩阵,权重展开成了12\times 2的矩阵,所以最后的结果是8\times 2的矩阵:
[[1035.| 2619.]
[1101.| 2829.]
[1233.| 3249.]
[1299.| 3459.]
------+-------
[2817.| 8289.]
[2883.| 8499.]
[3015.| 8919.]
[3081.| 9129.]]
- 两个样本的原始数组x展开后的矩阵
col_x是8\times 12,计算结果是8\times 2,如果原始数据只有一个样本,则展开矩阵col_x的形状是4\times 12,那么运算结果将会是4\times 2。所以,在上面这个8\times 2的矩阵中,前4行应该是第一个样本的卷积结果,后4行是第二个样本的卷积结果。 - 如果输出通道只有一个,则权重矩阵
w展开后的col_w只有一列,那么运算结果将会是8\times 1;两个输出通道的运算结果是8\times 2。所以第一列和第二列应该是两个通道的数据,而不是两个样本的数据。
也就是说,在这个数组中:
- 第1列的前4行是第1个样本的第1个通道的输出
- 第2列的前4行是第1个样本的第2个通道的输出
- 第1列的后4行是第2个样本的第1个通道的输出
- 第2列的后4行是第2个样本的第2个通道的输出
于是我们可以分两步得到正确的矩阵形状:
- 先把数据变成2个样本 * 输出高度 * 输出宽度的形状:
out2 = output.reshape(batch_size, output_height, output_width, -1)
得到结果:
out2=
[[[[1035. 2619.]
[1101. 2829.]]
[[1233. 3249.]
[1299. 3459.]]]
[[[2817. 8289.]
[2883. 8499.]]
[[3015. 8919.]
[3081. 9129.]]]]
注意现在1035和2619在一个子矩阵中,这是不对的,因为它们应该属于两个通道,所以应该在两个子矩阵中。目前这个结果中的四维数据的顺序是:样本、行、列、通道。于是我们做第二步,把“通道”所在的第4维移到第2维,变成:样本、通道、行、列:
- 把第4维数据放到第2维(由于是0-base的,所以是把第3维移到第1维的位置):
out3 = np.transpose(out2, axes=(0, 3, 1, 2))
结果是:
conv result=
(样本1) (样本2)
(通道1) (通道1)
[[[[1035. 1101.] [[[2817. 2883.]
[1233. 1299.]] [3015. 3081.]]
(通道2) (通道2)
[[2619. 2829.] [[8289. 8499.]
[3249. 3459.]]] [8919. 9129.]]]]
验证正确性⚓︎
我们可以用17.2.3中的方法1做为基准,如果用本节中的方法3可以得到同样的结果,就说明这种方式是正确的。
def test_4d_im2col():
......
f1 = c1.forward_numba(x)
f2 = c1.forward_img2col(x)
print("correctness:", np.allclose(f1, f2, atol=1e-7))
correctness: True
ConvLayer实例,然后分别调用内部实现的forward_numba()方法和forward_img2col()方法,得到f1和f2两个卷积结果矩阵,然后比较其数值,最后的返回值为True,说明im2col方法的正确性。
性能测试⚓︎
下面我们比较一下方法2和方法3的性能。
def test_performance():
...
print("compare correctness of method 1 and method 2:")
print("forward:", np.allclose(f1, f2, atol=1e-7))
上述代码先生成一个ConvLayer实例,然后分别调用1000次forward_numba()方法和1000次forward_img2col()方法,最后得到的结果是:
method numba: 11.663846492767334
method img2col: 14.926148653030396
compare correctness of method 1 and method 2:
forward: True
numba方法会比im2col方法快3秒,目前看来numba方法稍占优势。但是如果没有numba的帮助,im2col方法会比方法1快几百倍。
代码位置⚓︎
ch17, Level2
其中,Level2_Numba_Test.py是测试numba库的性能,Level2_Img2Col_Test是比较numba方法和im2col方法的前向计算性能。
在Level2的主过程中有4个函数:
test_2d_conv,理解2维下im2col的工作原理understand_4d_im2col,理解4维下im2col的工作原理test_4d_im2col,比较两种方法的结果,从而验证正确性test_performance,比较两种方法的性能