19.2 四个时间步的循环神经网络

19.2 四个时间步的循环神经网络

本小节中，我们将学习具有四个时间步的循环神经网络，用于二分类功能。

19.2.1 提出问题

在加减法运算中，总会遇到进位或者退位的问题，我们以二进制为例，比如13-6=7这个十进制的减法，变成二进制后如下所示：

13 - 6 = 7
====================
  x1: [1, 1, 0, 1]
- x2: [0, 1, 1, 0]
------------------
  y:  [0, 1, 1, 1]
====================

• 被减数13变成了[1, 1, 0, 1]
• 减数6变成了[0, 1, 1, 0]
• 结果7变成了[0, 1, 1, 1]

在减法过程中：

• x1和x2的最后一位是1和0，相减为1
• 倒数第二位是0和1，需要从前面借一位，相减后得1
• 倒数第三位本来是1和1，借位后变成了0和1，再从前面借一位，相减后得1
• 倒数第四位本来是1和0，借位后是0和0，相减为0

也就是说，在减法过程中，后面的计算会影响前面的值，所以必须逐位计算，这也就是时间步的概念，所以应该可以用循环神经网络的技术来解决。

19.2.2 准备数据

由于计算是从最后一位开始的，我们认为最后一位是第一个时间步，所以需要把样本数据的前后顺序颠倒一下，比如13，从二进制的 [1, 1, 0, 1] 倒序变成 [1, 0, 1, 1]。相应地，标签数据7也要从二进制的 [0, 1, 1, 1] 倒序变成 [1, 1, 1, 0]。

在这个例子中，因为是4位二进制减法，所以最大值是15，即 [1, 1, 1, 1]；最小值是0，并且要求被减数必须大于减数，所以样本的数量一共是136个，每个样本含有两组4位的二进制数，表示被减数和减数。标签值为一组4位二进制数。三组二进制数都是倒序。

所以，仍以13-6=7为例，单个样本如表19-4所示。

表19-4 以13-6=7为例的单个样本

时间步	特征值1	特征值2	标签值
1（最低位）	1	0	1
2	0	1	1
3	1	1	1
4（最高位）	1	0	0

为了和图19-11保持一致，我们令时间步从1开始（但编程时是从0开始的）。特征值1从下向上看是[1101]，即十进制13；特征值2从下向上看是[0110]，即十进制6；标签值从下向上看是[0111]，即十进制6。

所以，单个样本是一个二维数组，而多个样本就是三维数组，第一维是样本，第二维是时间步，第三维是特征值。

19.2.3 搭建多个时序的网络

搭建网络

在本例中，我们仍然从前馈神经网络的结构扩展到含有4个时序的循环神经网络结构，如图19-11所示。

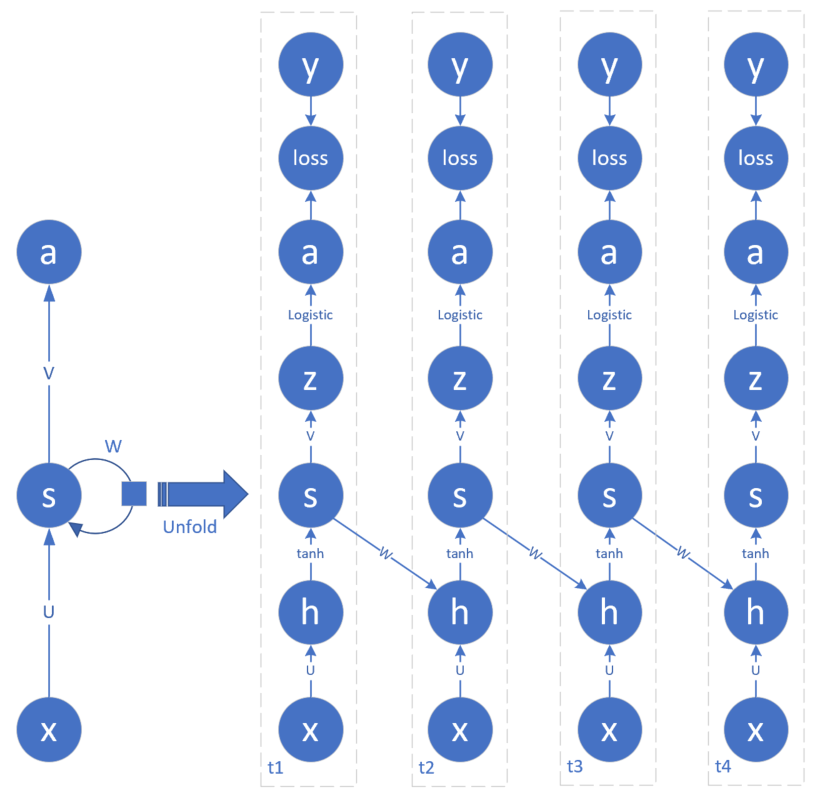
图19-11 含有4个时序的网络结构图

图19-11中，最左侧的简易结构是通常的循环神经网络的画法，而右侧是其展开后的细节，由此可见细节有很多，如果不展开的话，对于初学者来说很难理解，而且也不利于我们进行反向传播的推导。

与19.1节不同的是，在每个时间步的结构中，多出来一个a，是从z经过二分类函数生成的。这是为什么呢？因为在本例中，我们想模拟二进制数的减法，所以结果应该是0或1，于是我们把它看作是二分类问题，z的值是一个浮点数，用二分类函数后，使得a的值尽量向两端（0或1）靠近，但是并不能真正地达到0或1，只要大于0.5就认为是1，否则就认为是0。

二分类问题的损失函数使用交叉熵函数，这与我们在前面学习的二分类问题完全相同。

再重复一下，请读者记住，t1是二进制数的最低位，但是由于我们把样本倒序了，所以，现在的t1就是样本的第0个单元的值。并且由于涉及到被减数和减数，所以每个样本的第0个单元（时间步）都有两个特征值，其它3个单元也一样。

在19.1节的例子中，连接x和h的是一条线标记为U，U是一个标量参数；在图19-11中，由于隐层神经元数量为4，所以U是一个 1x4 的参数矩阵，V是一个 4x1 的参数矩阵，而W就是一个 4x4 的参数矩阵。我们把它们展开画成图19-12（其中把s和h合并在一起了）。

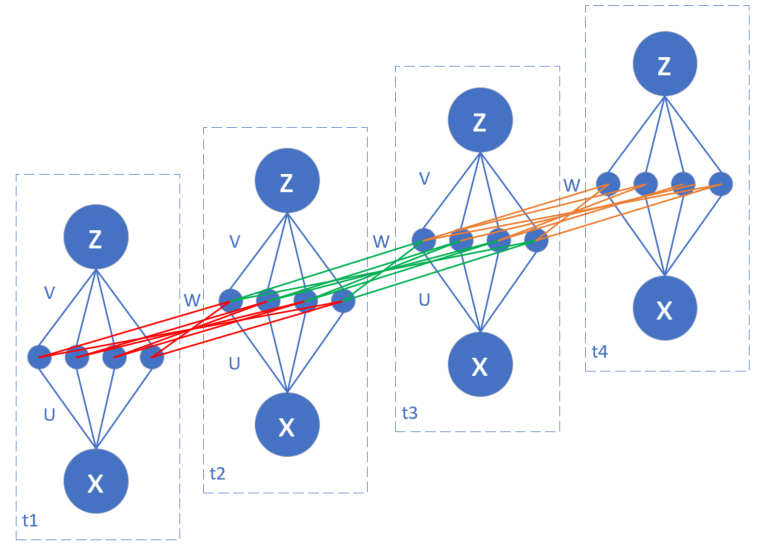
图19-12 W权重矩阵的展开图

U和V都比较容易理解，而W是一个连接相邻时序的参数矩阵，并且共享相同的参数值，这一点在刚开始接触循环神经网络时不太容易理解。图19-12中把W绘制成3种颜色，代表它们在不同的时间步中的作用，是想让读者看得清楚些，并不代表它们是不同的值。

19.2.4 正向计算

下面我们先看看4个时序的正向计算过程。

从图一中看，t2、t3、t4的结构是一样的，只有t1缺少了从前面的时间步的输入，因为它是第一个时序，前面没有输入，所以我们单独定义t1的前向计算函数：

$$h = x \cdot U \tag{1}$$

$$s = Tanh(h) \tag{2}$$

$$z = s \cdot V \tag{3}$$

$$a = Logistic(z) \tag{4}$$

在公式1和公式3中，我们并没有添加偏移项b，是因为在此问题中，没有偏移项一样可以完成任务。

单个时间步的损失函数值：

$$loss_t = -[y_t \ln a_t + (1-y_t) \ln (1-a_t)]$$

所有时间步的损失函数值计算：

$$Loss = \frac{1}{4} \sum_{t=1}^4 loss_t \tag{5}$$

公式5中的$Loss$表示每个时间步的$loss_t$之和。

class timestep_1(timestep):
    def forward(self,x,U,V,W):
        self.U = U
        self.V = V
        self.W = W
        self.x = x
        # 公式1
        self.h = np.dot(self.x, U)
        # 公式2
        self.s = Tanh().forward(self.h)
        # 公式3
        self.z = np.dot(self.s, V)
        # 公式4
        self.a = Logistic().forward(self.z)

其它三个时间步的前向计算过程是一样的，它们与t1的不同之处在于公式1，所以我们单独说明一下：

$$h = x \cdot U + s_{t-1} \cdot W \tag{6}$$

class timestep(object):
    def forward(self,x,U,V,W,prev_s):
        ...
        # 公式6
        self.h = np.dot(x, U) + np.dot(prev_s, W)
        ...

19.2.5 反向传播

反向传播的计算对于4个时间步来说，分为3种过程，但是它们之间只有微小的区别。我们先把公共的部分列出来，再说明每个时间步的差异。

首先是损失函数对z节点的偏导数，对于4个时间步来说都一样：

$$\begin{aligned} \frac{\partial loss_t}{\partial z_t}&=\frac{\partial loss_t}{\partial a_t}\frac{\partial a_t}{\partial z_t} \\\\ &= a_t - y_t \rightarrow dz_t \end{aligned} \tag{7}$$

再进一步计算s和h的误差。对于t4来说，s和h节点的路径比较单一，直接从z节点向下反向推导即可：

$$\frac{\partial loss_{t4}}{\partial s_{t4}}=\frac{\partial loss_{t4}}{\partial z_{t4}}\frac{\partial z_{t4}}{\partial s_{t4}} = dz_{t4} \cdot V^{\top} \tag{8}$$

$$\frac{\partial loss_{t4}}{\partial h_{t4}}=\frac{\partial loss_{t4}}{\partial s_{t4}}\frac{\partial s_{t4}}{\partial h_{t4}}=dz_{t4} \cdot V^{\top} \odot Tanh'(s_{t4}) \rightarrow dh_{t4} \tag{9}$$

提醒两点：

1. 公式8、9中用了$loss_{t4}$而不是$Loss$，因为只针对第4个时间步，而不是所有时间步。
2. 出现了$V^{\top}$，因为在本例中V是一个矩阵，而非标量，在求导时需要转置。

对于t1、t2、t3的s节点来说，都有两个方向的反向路径，第一个是从本时间步的z节点，第二个是从后一个时间步的h节点，因此，s的反向计算应该是两个路径的和。

我们先以t3为例推导：

$$\begin{aligned} \frac{\partial Loss}{\partial s_{t3}}&=\frac{\partial loss_{t3}}{\partial s_{t3}} + \frac{\partial loss_{t4}}{\partial s_{t3}} \\\\ &=\frac{\partial loss_{t3}}{\partial s_{t3}} + \frac{\partial loss_{t4}}{\partial h_{t4}}\frac{\partial h_{t4}}{\partial s_{t3}} \\\\ &=dz_{t3} \cdot V^{\top} + dh_{t4} \cdot W^{\top} \end{aligned}$$

再扩展到一般情况：

$$\begin{aligned} \frac{\partial Loss}{\partial s_t}&=\frac{\partial loss_t}{\partial s_t} + \frac{\partial Loss}{\partial h_{t+1}}\frac{\partial h_{t+1}}{\partial s_t} \\\\ &=dz_t \cdot V^{\top} + dh_{t+1} \cdot W^{\top} \end{aligned} \tag{10}$$

再进一步计算t1、t2、t3的h节点的误差：

$$\begin{aligned} \frac{\partial Loss}{\partial h_t} &= \frac{\partial Loss}{\partial s_t} \frac{\partial s_t}{\partial h_t} \\\\ &= (dz \cdot V^{\top} + dh_{t+1} \cdot W^{\top} ) \odot Tanh'(s_t) \rightarrow dh_t \end{aligned} \tag{11}$$

下面计算V的误差，V只与z节点和s节点有关，而且4个时间步是相同的：

$$\frac{\partial loss_t}{\partial V_t}=\frac{\partial loss_t}{\partial z_t}\frac{\partial z_t}{\partial V_t}=s_t^{\top} \cdot dz_t \rightarrow dV_t \tag{12}$$

下面计算U的误差，U只与节点h和输入x有关，而且4个时间步是相同的，但是U参与了所有时间步的计算，因此要用 $Loss$ 求 $U_t$ 的偏导：

$$\frac{\partial Loss}{\partial U_t}=\frac{\partial Loss}{\partial h_t}\frac{\partial h_t}{\partial U_t}=x_t^{\top} \cdot dh_t \rightarrow dU_t \tag{13}$$

下面计算W的误差，从图19-11中看，t1没有W参与计算的，与其它三个时间步不同，所以对于t1来说：

$$dW_{t1} = 0 \tag{14}$$

对于t2、t3、t4：

$$\frac{\partial Loss}{\partial W_t}=\frac{\partial Loss}{\partial h_t}\frac{\partial h_t}{\partial W_t}=s_{t-1}^{\top} \cdot dh_{t} \rightarrow dW_{t} \tag{15}$$

下面是t1的反向传播函数，与其他3个t不同的是dW部分为0：

class timestep_1(timestep):
    def backward(self, y, next_dh):
        ...
        self.dh = (np.dot(self.dz, self.V.T) + np.dot(next_dh, self.W.T)) * Tanh().backward(self.s)
        self.dW = 0

下面是t2、t3的反向传播函数：

class timestep(object):
    def backward(self, y, prev_s, next_dh):
        ...
        self.dh = (np.dot(self.dz, self.V.T) + np.dot(next_dh, self.W.T)) * Tanh().backward(self.s)
        self.dW = np.dot(prev_s.T, self.dh)

下面是t4的反向传播函数，与前三个t不同的是dh的求导公式中少一项：

class timestep_4(timestep):
    # compare with timestep class: no next_dh from future layer
    def backward(self, y, prev_s):
        ...
        self.dh = np.dot(self.dz, self.V.T) * Tanh().backward(self.s)
        self.dW = np.dot(prev_s.T, self.dh)

19.2.6 梯度更新

到目前为止，我们已经得到了所有时间步的关于所有参数的梯度，梯度更新时，由于参数共享，所以与19.1节中的方法一样，先要把所有时间步的相同参数的梯度相加，统一乘以学习率，与上一次的参数相减。

用一个通用的公式描述：

$$W_{next} = W_{current} - \eta \cdot \sum_{t=1}^{\tau} dW_t$$

其中，$W$可以换成 $U、V$ 等参数。

19.2.7 代码实现

在上一小节我们已经讲解了正向和反向的代码实现，本小节讲一下训练部分的主要代码。

初始化

初始化 loss function 和 loss trace，然后初始化4个时间步的实例。注意t2和t3使用了相同的类timestep。

class net(object):
    def __init__(self, dr):
        ...
        self.t1 = timestep_1()
        self.t2 = timestep()
        self.t3 = timestep()
        self.t4 = timestep_4()

前向计算

按顺序分别调用4个时间步的前向计算函数，注意在t2到t4时，需要把t-1时刻的s值代进去。

    def forward(self,X):
        self.t1.forward(X[:,0],self.U,self.V,self.W)
        self.t2.forward(X[:,1],self.U,self.V,self.W,self.t1.s)
        self.t3.forward(X[:,2],self.U,self.V,self.W,self.t2.s)
        self.t4.forward(X[:,3],self.U,self.V,self.W,self.t3.s)

反向传播

按相反的顺序调用4个时间步的反向传播函数，注意在t3、t2、t1时，要把t+1时刻的dh代进去，以便计算当前时刻的dh；而在t4、t3、t2时，需要把t-1时刻的s值代进去，以便计算dW的值。

    def backward(self,Y):
        self.t4.backward(Y[:,3], self.t3.s)
        self.t3.backward(Y[:,2], self.t2.s, self.t4.dh)
        self.t2.backward(Y[:,1], self.t1.s, self.t3.dh)
        self.t1.backward(Y[:,0],            self.t2.dh)

更新参数

在参数更新部分，需要把4个时间步的参数梯度相加再乘以学习率，做为整个网络的梯度。

    def update(self, eta):
        self.U = self.U - (self.t1.dU + self.t2.dU + self.t3.dU + self.t4.dU)*eta
        self.V = self.V - (self.t1.dV + self.t2.dV + self.t3.dV + self.t4.dV)*eta
        self.W = self.W - (self.t1.dW + self.t2.dW + self.t3.dW + self.t4.dW)*eta

损失函数

4个时间步都参与损失函数计算，所以总体的损失函数是4个时间步的损失函数值的和。

    def check_loss(self,X,Y):
        ......
        Loss = (loss1 + loss2 + loss3 + loss4)/4
        return Loss,acc,result

训练过程

用双重循环进行训练，每次只用一个样本，因此batch_size=1。

    def train(self, batch_size, checkpoint=0.1):
        ...
        for epoch in range(max_epoch):
            dr.Shuffle()
            for iteration in range(max_iteration):
                # get data
                batch_x, batch_y = self.dr.GetBatchTrainSamples(1, iteration)
                # forward
                self.forward(batch_x)
                # backward
                self.backward(batch_y)
                # update
                self.update(eta)
                # check loss            
              ...

19.2.8 运行结果

我们设定在验证集上的准确率为1.0时即停止训练，图19-13为训练过程曲线。

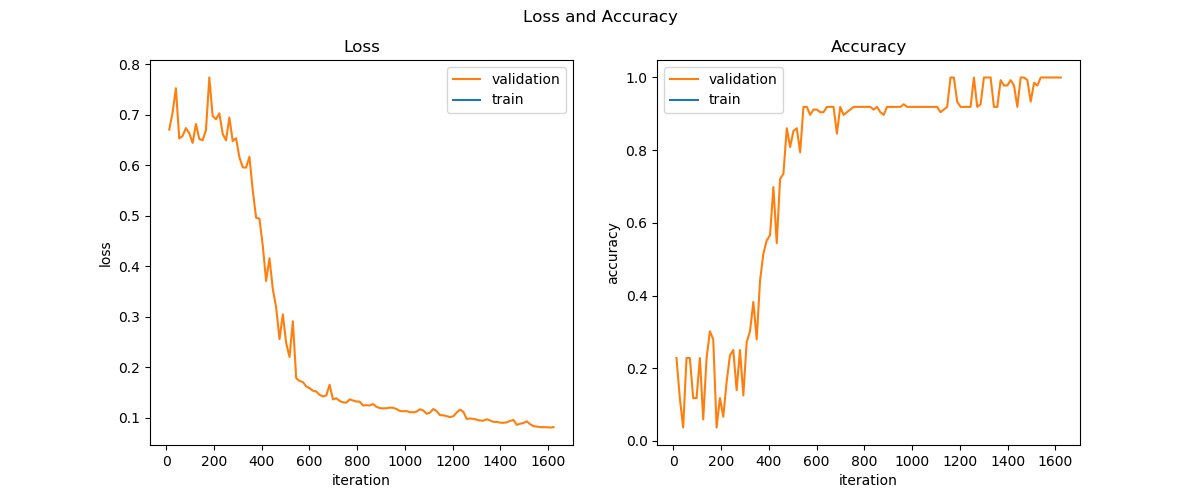
图19-13 训练过程中的损失函数和准确率变化

下面是最后几轮的打印输出结果：

...
5 741 loss=0.156525, acc=0.867647
5 755 loss=0.131925, acc=0.963235
5 811 loss=0.106093, acc=1.000000
testing...
loss=0.105319, acc=1.000000

我们在验证集上（实际上和测试集一致）得到了100%的准确率，即所有136个测试样本都可以得到正确的预测值。

下面随机列出了几个测试样本及其预测结果：

  x1: [1, 0, 1, 1]
- x2: [0, 0, 0, 1]
------------------
true: [1, 0, 1, 0]
pred: [1, 0, 1, 0]
11 - 1 = 10
====================

  x1: [1, 1, 1, 1]
- x2: [0, 0, 1, 1]
------------------
true: [1, 1, 0, 0]
pred: [1, 1, 0, 0]
15 - 3 = 12
====================

  x1: [1, 1, 0, 1]
- x2: [0, 1, 1, 0]
------------------
true: [0, 1, 1, 1]
pred: [0, 1, 1, 1]
13 - 6 = 7
====================

我们如何理解循环神经网络的概念在这个问题中的作用呢？

在每个时间步中，U、V负责的是0、1相减可以得到正确的值，而W的作用是借位，在相邻的时间步之间传递借位信息，以便当t-1时刻的计算发生借位时，在t时刻也可以得到正确的结果。

代码位置

ch19, Level2

思考和练习

1. 把tanh函数变成sigmoid函数，试试看有什么不同？
2. 给h和z节点增加偏移值，看看有什么不同？
3. 把h节点的神经元数量增加到8个或16个，看看训练过程有何不同？减少到2个神经元会得到正确结果吗？
4. 把二进制数扩展为8位，即最大值255时，这个网络还能正确工作吗？