19.5 不定长时序的循环神经网络

19.5 不定长时序的循环神经网络⚓︎

本小节中，我们将学习具有不固定的时间步的循环神经网络网络，用于多分类功能。

19.5.1 提出问题⚓︎

各个国家的人都有自己习惯的一些名字，下面列举出了几个个国家/语种的典型名字 $^{[1]}$ ：

Guan    Chinese
Rong    Chinese
Bond    English
Stone   English
Pierre  French
Vipond  French
Metz    German
Neuman  German
Aggio   Italian
Falco   Italian
Akimoto Japanese
Hitomi  Japanese

名字都是以ASCII字母表示的，以便于不同语种直接的比较。

如果隐藏掉第二列，只看前面的名字的话，根据发音、拼写习惯等，我们可以大致猜测出这些名字属于哪个国家/语种。当然也有一些名字是重叠的，比如“Lang”，会同时出现在English、Chinese、German等几种语种里。

既然人类可以凭借一些模糊的知识分辨名字与国家/语种的关系，那么神经网络能否也具备这个能力呢？

下面我们仍然借助于循环神经网络来完成这个任务。

19.5.2 准备数据⚓︎

下载数据⚓︎

从这里 "https://download.pytorch.org/tutorial/data.zip" 下载数据到本地，然后解压缩出其中的 "data\names\" 目录下的所有文件到 "ch19-RNNBasic\ExtendedDataReader\data\names" 中。

然后运行 ch19_NameClassifier_data.py，将会在 "ch19-RNNBasic\ExtendedDataReader\data\" 目录中生成一个文件：ch19.name_language.txt。

循环神经网络的要点是“循环”二字，也就是说一个样本中的数据要分成连续若干个时间步，然后逐个“喂给”网络进行训练。如果两个样本的时间步总数不同，是不能做为一个批量一起喂给网络的，比如一个名字是Rong，另一个名字是Aggio，这两个名字不能做为一批计算。

在本例中，由于名字的长度不同，所以不同长度的两个名字，是不能放在一个batch里做批量运算的。但是如果一个一个地训练样本，将会花费很长的时间，所以需要我们对本例中的数据做一个特殊的处理：

先按字母个数（名字的长度）把所有数据分开，由于最短的名字是2个字母，最长的是19个字母，所以一共应该有18组数据（实际上只有15组，中间有些长度的名字不存在）。
使用OneHot编码把名字转换成向量，比如：名字为“Duan”，变成小写字母“duan”，则OneHot编码是：

[[0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],  # d
 [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0],  # u
 [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],  # a
 [0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0]]  # n

把所有相同长度的名字的OneHot编码都堆放在一个矩阵中，形成批量，这样就是成为了一个三维矩阵：
第一维是名字的数量，假设一共有230个4个字母的名字，175个5个字母的名字，等等；
第二维是4或者5或者其它值，即字母个数，也是时间步的个数；
第三维是26，即a~z的小写字母的个数，相应的位为1，其它位为0。

在用SGD方法训练时，先随机选择一个组，假设是6个字母的名字，再从这一组中随机选择一个小批量，比如8个名字，这样就形成了一个8x6x26的三维批量数据。如果随机选到了7个字母的组，最后会形成8x7x26的三维批量数据。

19.5.3 搭建不定长时序的网络⚓︎

搭建网络⚓︎

为什么是不定长时序的网络呢？因为名字的单词中的字母个数不是固定的，最少的两个字母，最多的有19个字母。

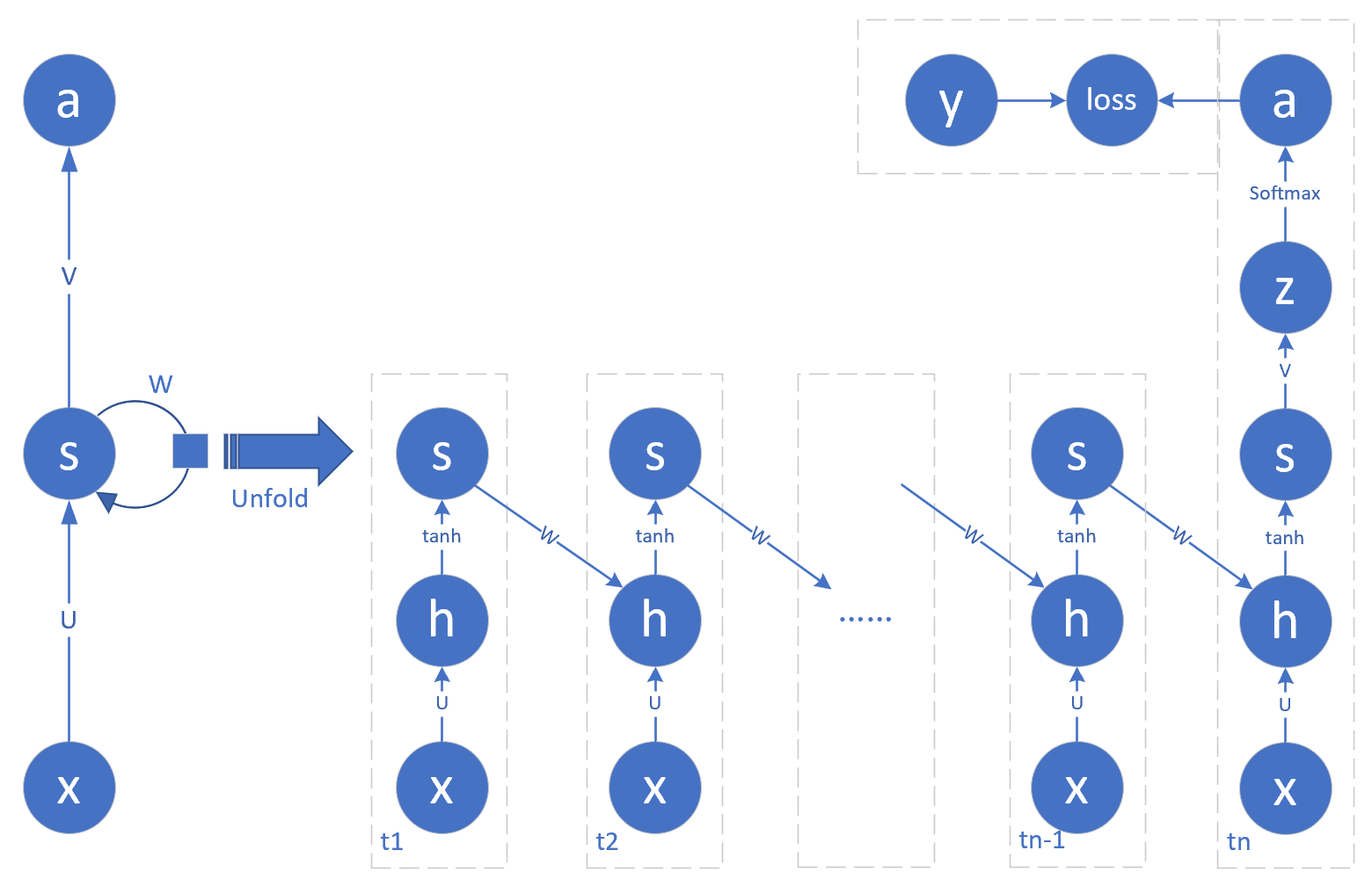
图19-18 不定长时间步的网络

在图19-18中，n=19，可以容纳19个字母的单词。为了节省空间，把最后一个时间步的y和loss画在了拐弯的位置。

并不是所有的时序都需要做分类输出，而是只有最后一个时间步需要。比如当名字是“guan”时，需要在第4个时序做分类输出，并加监督信号做反向传播，而前面3个时序不需要。但是当名字是“baevsky”时，需要在第7个时间步做分类输出。所以n值并不是固定的。

对于最后一个时间步，展开成前馈神经网络中的标准Softmax多分类。

前向计算⚓︎

在第19.3中已经介绍过通用的方法，所以不再赘述。本例中的特例是分类函数使用Softmax，损失函数使用多分类交叉熵函数：

$a = Softmax(z) \tag{1}$

$Loss = loss_{\tau} = -y \odot \ln a \tag{2}$

反向传播⚓︎

反向传播的推导和前面两节区别不大，唯一的变化是Softmax接多分类交叉熵损失函数，但这也是我们在前馈神经网络中学习过的。

19.5.4 代码实现⚓︎

其它部分的代码都大同小异，只有主循环部分略有不同：

    def train(self, dataReader, checkpoint=0.1):
        ...
        for epoch in range(self.hp.max_epoch):
            self.hp.eta = self.lr_decay(epoch)
            dataReader.Shuffle()
            while(True):
                batch_x, batch_y = dataReader.GetBatchTrainSamples(self.hp.batch_size)
                if (batch_x is None):
                    break
                self.forward(batch_x)
                self.backward(batch_y)
                self.update()
        ...

获得批量训练数据函数，可以保证取到相同时间步的一组样本，这样就可以进行批量训练了，提高速度和准确度。如果取回None数据，说明所有样本数据都被使用过一次了，则结束本轮训练，检查损失函数值，然后进行下一个epoch的训练。

19.5.5 运行结果⚓︎

我们需要下面一组超参来控制模型训练：

    eta = 0.02
    max_epoch = 100
    batch_size = 8
    num_input = dataReader.num_feature
    num_hidden = 16
    num_output = dataReader.num_category

几个值得注意的地方是：

学习率较大或者batch_size较小时，会造成网络不收敛，损失函数高居不下，或者来回震荡；
隐层神经元数量为16，虽然输入的x的特征值向量数为26，但却是OneHot编码，有效信息很少，所以不需要很多的神经元数量。

最后得到的损失函数曲线如图19-19所示。可以看到两条曲线的抖动都比较厉害，此时可以适当地降低学习率来使曲线平滑，收敛趋势稳定。

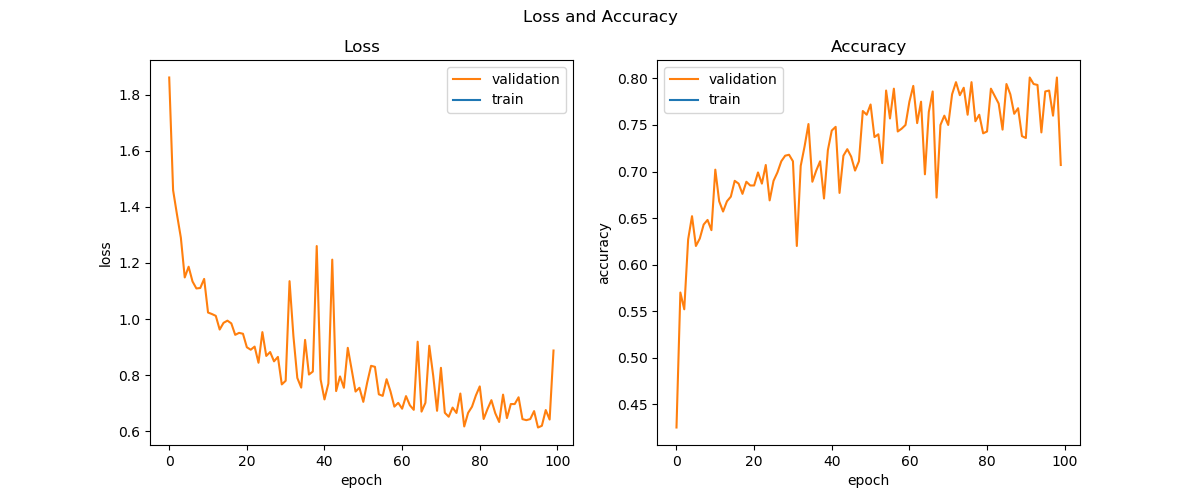
图19-19 训练过程中的损失函数值和准确度的变化

本例没有独立的测试数据，所以最后是在训练数据上做的测试，打印输出如下所示：

...
99:55800:0.02 loss=0.887763, acc=0.707000
correctness=2989/4400=0.6793181818181818
load best parameters...
correctness=3255/4400=0.7397727272727272

训练100个epoch后得到的准确率为67.9%，其间我们保存了损失函数值最小的时刻的参数矩阵值，使用load best parameters方法后，再次测试，得到73.9%的准确率。

由于是多分类问题，所以我们尝试使用混淆矩阵的方式来分析结果。

表19-9

最后的效果	最好的效果

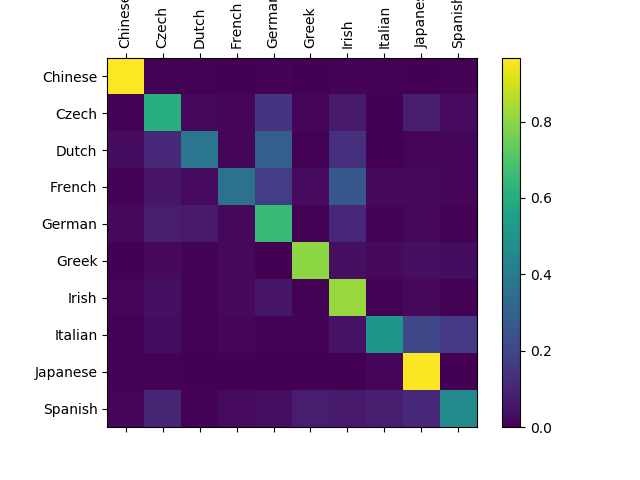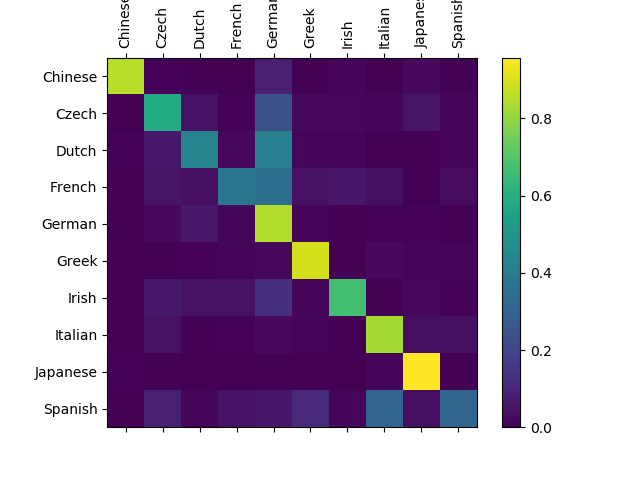准确率为67.9%的混淆矩阵	准确率为73.9%的混淆矩阵

在表19-9中的图中，对角线上的方块越亮，表示识别越准确。

左图，对于Dutch，被误识别为German类别的数量不少，所以Dutch-German交叉点的方块较亮，原因是German的名字确实比较多，两国的名字比较相近，使用更好的超参或更多的迭代次数可以改善。而French被识别为Irish的也比较多。

表19-9右图，可以看到非对角线位置的可见方块的数量明显减少，这也是准确率高的体现。

代码位置⚓︎

ch19, Level5

参考资料⚓︎

[1] PyTorch Sample, link: https://pytorch.org/tutorials/intermediate/char_rnn_classification_tutorial.html