20.1 LSTM基本原理

20.1 LSTM基本原理

本小节中，我们将学习长短时记忆（Long Short Term Memory, LSTM）网络的基本原理。

20.1.1 提出问题

循环神经网络（RNN）的提出，使神经网络可以训练和解决带有时序信息的任务，大大拓宽了神经网络的使用范围。但是原始的RNN有明显的缺陷。不管是双向RNN，还是深度RNN，都有一个严重的缺陷：训练过程中经常会出现梯度爆炸和梯度消失的问题，以至于原始的RNN很难处理长距离的依赖。

从实例角度

例如，在语言生成问题中：

佳佳今天帮助妈妈洗碗，帮助爸爸修理椅子，还帮助爷爷奶奶照顾小狗毛毛，大家都夸奖了 $\underline{\qquad\quad}$。

例句中出现了很多人，空白出要填谁呢？我们知道是“佳佳”，传统RNN无法很好学习这么远距离的依赖关系。

从理论角度

根据循环神经网络的反向传播算法，可以得到任意时刻k, 误差项沿时间反向传播的公式如下： $$ \delta^T_k=\deltaT_t \prod_{i=k}^{t-1} diag[f'(z_i)]W $$

其中 $f$为激活函数，$z_i$为神经网络在第$i$时刻的加权输入， $W$为权重矩阵，$diag$表示一个对角矩阵。

注意，由于使用链式求导法则，式中有一个连乘项 $\prod_{i=k}^{t-1} diag[f'(z_i)]W$ , 如果激活函数是挤压型，例如 $Tanh$ 或 $sigmoid$ , 他们的导数值在 [0,1] 之间。我们再来看$W$。 1. 如果$W$的值在 (0,1) 的范围内， 则随着$t$的增大，连乘项会越来越趋近于0， 误差无法传播，这就导致了 梯度消失 的问题。 2. 如果$W$的值很大，使得$diag[f'(z_i)]W$的值大于$1$， 则随着$t$的增大，连乘项的值会呈指数增长，并趋向于无穷，产生 梯度爆炸。

梯度消失使得误差无法传递到较早的时刻，权重无法更新，网络停止学习。梯度爆炸又会使网络不稳定，梯度过大，权重变化太大，无法很好学习，最坏情况还会产生溢出（NaN）错误而无法更新权重。

解决办法

为了解决这个问题，科学家们想了很多办法。

1. 采用半线性激活函数ReLU代替 挤压型激活函数，ReLU函数在定义域大于0的部分，导数恒等于1，来解决梯度消失问题。
2. 合理初始化权重$W$，使$diag[f'(z_i)]W$的值尽量趋近于1，避免梯度消失和梯度爆炸。

上面两种办法都有一定的缺陷，ReLU函数有自身的缺点，而初始化权重的策略也抵不过连乘操作带来的指数增长问题。要想根本解决问题，必须去掉连乘项。

科学家们冥思苦想，终于提出了新的模型 —— 长短时记忆网络（LSTM）。

20.1.2 LSTM网络

20.1.2.1 LSTM的结构

LSTM 的设计思路比较简单，原来的RNN中隐藏层只有一个状态h，对短期输入敏感，现在再增加一个状态c，来保存长期状态。这个新增状态称为 细胞状态（cell state）**或**单元状态。 增加细胞状态前后的网络对比，如图20-1，20-2所示。

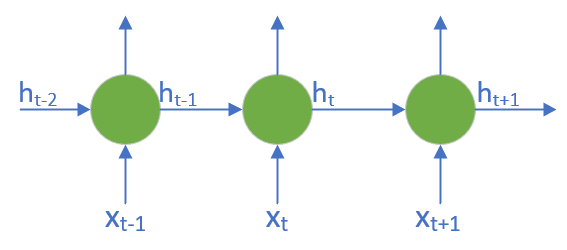
图20-1 传统RNN结构示意图

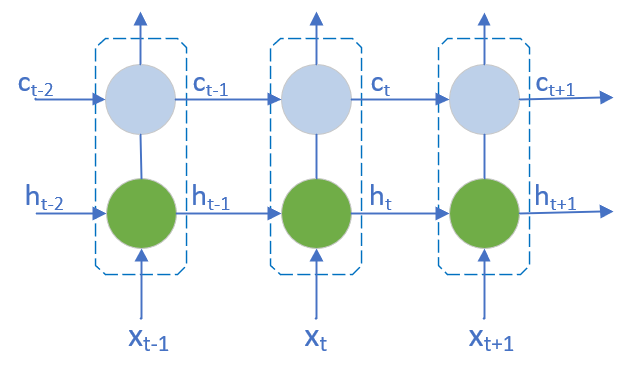
图20-2 LSTM结构示意图

那么，如何控制长期状态c呢？在任意时刻$t$，我们需要确定三件事：

1. $t-1$时刻传入的状态$c_{t-1}$，有多少需要保留。
2. 当前时刻的输入信息，有多少需要传递到$t+1$时刻。
3. 当前时刻的隐层输出$h_t$是什么。

LSTM设计了 门控（gate） 结构，控制信息的保留和丢弃。LSTM有三个门，分别是：遗忘门（forget gate），输入门（input gate）和输出门（output gate）。

图20-3是常见的LSTM结构，我们以任意时刻t的一个LSTM单元（LSTM cell）为例，来分析其工作原理。

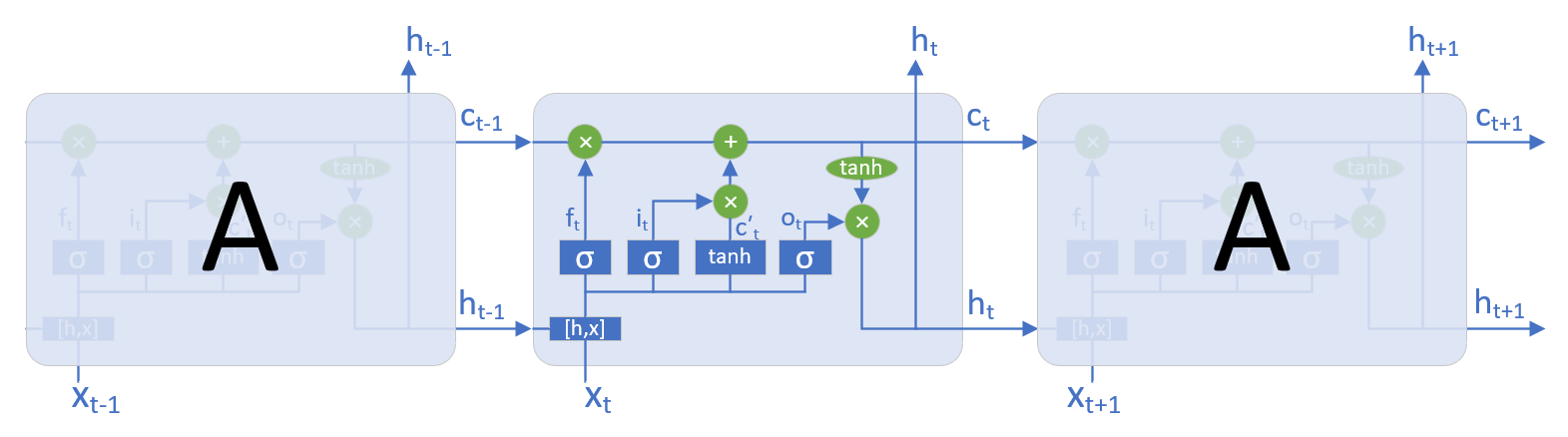
图20-3 LSTM内部结构意图

20.1.2.2 LSTM的前向计算

1. 遗忘门

   由上图可知，遗忘门的输出为$f_t$， 采用sigmoid激活函数，将输出映射到[0,1]区间。上一时刻细胞状态$c_{t-1}$通过遗忘门时，与$f_t$结果相乘，显然，乘数为0的信息被全部丢弃，为1的被全部保留。这样就决定了上一细胞状态$c_{t-1}$有多少能进入当前状态$c_t$。

   遗忘门$f_t$的公式如下：

   $$f_t = \sigma(h_{t-1} \cdot W_f + x_t \cdot U_f + b_f) \tag{1}$$

   其中，$\sigma$为sigmoid激活函数，$h_{t-1}$ 为上一时刻的隐层状态，形状为$(1 \times h)$的行向量。$x_t$为当前时刻的输入，形状为$(1 \times i)$的行向量。参数矩阵$W_f$、$U_f$分别是$(h \times h)$和$(i \times h)$的矩阵，$b_f$为$(1 \times h)$的行向量。

   很多教科书或网络资料将公式写成如下格式：

   $$f_t=\sigma(W_f\cdot[h_{t-1}, x_t] + b_f) \tag{1'}$$

   或

   $$\begin{aligned} f_t &= \sigma([W_{fh}\;W_{fx}] \begin{bmatrix}h_{t-1}\\\\x_t \end{bmatrix}+b_f) \\\\ &= \sigma(W_{fh}h_{t-1}+W_{fx}x_t+b_f) \end{aligned} \tag{1''}$$

   后两种形式将权重矩阵放在状态向量前面，在讲解原理时，与公式$(1)$没有区别，但在代码实现时会出现一些问题，所以，在本章中我们采用公式$(1)$的表达方式。

2. 输入门

   输入门$i_t$决定输入信息有哪些被保留，输入信息包含当前时刻输入和上一时刻隐层输出两部分，存入即时细胞状态$\tilde{c}_t$中。输入门依然采用sigmoid激活函数，将输出映射到[0,1]区间。$\tilde{c}_t$通过输入门时进行信息过滤。

   输入门$i_t$的公式如下：

   $$i_t = \sigma(h_{t-1} \cdot W_i + x_t \cdot U_i + b_i) \tag{2}$$

   即时细胞状态 $\tilde{c}_ t$的公式如下:

   $$\tilde c_t = \tanh(h_{t-1} \cdot W_c + x_t \cdot U_c + b_c) \tag{3}$$

   上一时刻保留的信息，加上当前输入保留的信息，构成了当前时刻的细胞状态$c_t$。

   当前细胞状态$c_t$的公式如下：

   $$c_t = f_t \circ c_{t-1}+i_t \circ \tilde{c}_t \tag{4}$$

   其中，符号 $\cdot$ 表示矩阵乘积， $\circ$ 表示 Hadamard 乘积，即元素乘积。

3. 输出门

   最后，需要确定输出信息。

   输出门$o_t$决定 $h_{t-1}$ 和 $x_t$ 中哪些信息将被输出，公式如下：

   $$o_t = \sigma(h_{t-1} \cdot W_o + x_t \cdot U_o + b_o) \tag{5}$$

   细胞状态$c_t$通过tanh激活函数压缩到 (-1, 1) 区间，通过输出门，得到当前时刻的隐藏状态$h_t$作为输出，公式如下：

   $$ h_t=o_t \circ \tanh(c_t) \tag{6} $$s

最后，时刻t的预测输出为：

$$a_t = \sigma(h_t \cdot V + b) \tag{7}$$

其中，

$$z_t = h_t \cdot V + b \tag{8}$$

经过上面的步骤，LSTM就完成了当前时刻的前向计算工作。

20.1.2.3 LSTM的反向传播

LSTM使用时序反向传播算法（Backpropagation Through Time, BPTT）进行计算。图20-4是带有一个输出的LSTM cell。我们使用该图来推导反向传播过程。

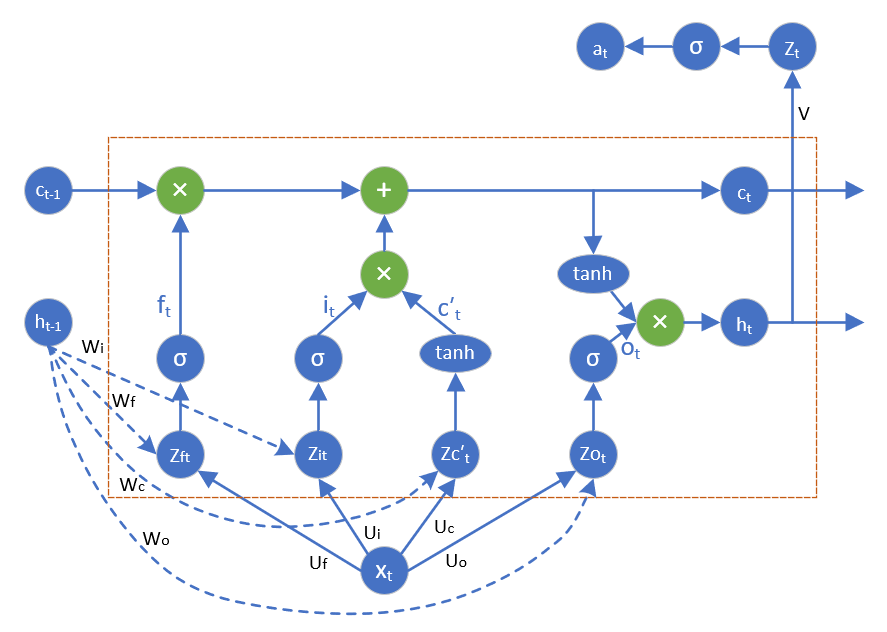
图20-4 带有一个输出的LSTM单元

假设当前LSTM cell处于第$l$层、$t$时刻。那么，它从两个方向接受反向传播的误差：一个是从$t+1$时刻$l$层传回的误差，记为$\delta^ l_{h_t}$（注意，这里的下标不是$h_{t+1}$，而是$h_t$）；另一个是从$t$时刻$l+1$层的输入传回误差，记为 $\delta^ {l+1}_{x_t}$。

我们先复习几个在推导过程中会使用到的激活函数，以及其导数公式。令sigmoid = $\sigma$，则：

$$\sigma(z) = y = \frac{1}{1+e^{-z}} \tag{9}$$

$$\sigma^{\prime}(z) = y(1-y) \tag{10}$$

$$\tanh(z) = y = \frac{e^z - e^{-z}}{e^z + e^{-z}} \tag{11}$$

$$\tanh^{\prime}(z) = 1-y^2 \tag{12}$$

假设某一线性函数 $z_i$ 经过Softmax函数之后的预测输出为 $\hat{y}_ i$，该输出的标签值为 $y_i$，则：

$$softmax(z_i) = \hat y_i = \frac{e^{z_i}}{\sum_{j=1}^me^{z_j}} \tag{13}$$

$$\frac{\partial{loss}}{\partial{z_i}} = \hat{y}_ i - y_i \tag{14}$$

从图中可知，从上层传回的误差为输出层$z_t$向$h^l_t$传回的误差，假设输出层的激活函数为softmax函数，输出层标签值为$y$，则：

$$\delta^{l+1}_ {x_t} = \frac{\partial{loss}}{\partial{z_t}} \cdot \frac{\partial{z_t}}{\partial{h^l_t}} = (a - y) \cdot V^{\top} \tag{15}$$

从$t+1$时刻传回的误差为$\delta^l_{h_t}$，若$t$为时序的最后一个时间点，则$\delta^l_{h_t}=0$。

该cell的隐层$h^l_t$的最终误差为两项误差之和，即：

$$\delta^l_t = \frac{\partial{loss}}{\partial{h_t}} = \delta^l_{h_t} + \delta^{l+1}_{x_t} = (a - y) \cdot V^{\top} \tag{16}$$

接下来的推导过程仅与本层相关，为了方便推导，我们忽略层次信息，令$\delta^l_t = \delta_t$。

可以求得各个门结构加权输入的误差，如下：

$$\begin{aligned} \delta_{z_{ot}} &= \frac{\partial{loss}}{\partial{z_{o_t}}} = \frac{\partial{loss}}{\partial{h_t}} \cdot \frac{\partial{h_t}}{\partial{o_t}} \cdot \frac{\partial{o_t}}{\partial{z_{o_t}}} \\\\ &= \delta_t \cdot diag[\tanh(c_t)] \cdot diag[o_t \circ (1 - o_t)] \\\\ &= \delta_t \circ \tanh(c_t) \circ o_t \circ (1 - o_t) \end{aligned} \tag{17}$$

$$\begin{aligned} \delta_{c_t} &= \frac{\partial{loss}}{\partial{c_t}} = \frac{\partial{loss}}{\partial{h_t}} \cdot \frac{\partial{h_t}}{\partial{\tanh(c_t)}} \cdot \frac{\partial{\tanh(c_t)}}{\partial{c_t}} \\\\ &= \delta_t \cdot diag[o_t] \cdot diag[1-\tanh^2(c_t)] \\\\ &= \delta_t \circ o_t \circ (1-\tanh^2(c_t)) \end{aligned} \tag{18}$$

$$\begin{aligned} \delta_{z_{\tilde{c}t}} &= \frac{\partial{loss}}{\partial{z_{\tilde c_t}}} = \frac{\partial{loss}}{\partial{c_t}} \cdot \frac{\partial{c_t}}{\partial{\tilde c_t}} \cdot \frac{\partial{\tilde c_t}}{\partial{z_{\tilde c_t}}} \\ &= \delta_{c_t} \cdot diag[i_t] \cdot diag[1-(\tilde c_t)^2] \\ &= \delta_{c_t} \circ i_t \circ (1-(\tilde c_t)^2) \end{aligned} \tag{19}$$

$$\begin{aligned} \delta_{z_{it}} &= \frac{\partial{loss}}{\partial{z_{i_t}}} = \frac{\partial{loss}}{\partial{c_t}} \cdot \frac{\partial{c_t}}{\partial{i_t}} \cdot \frac{\partial{i_t}}{\partial{z_{i_t}}} \\ &= \delta_{c_t} \cdot diag[\tilde c_t] \cdot diag[i_t \circ (1 - i_t)] \\ &= \delta_{c_t} \circ \tilde c_t \circ i_t \circ (1 - i_t) \end{aligned} \tag{20}$$

$$\begin{aligned} \delta_{z_{ft}} &= \frac{\partial{loss}}{\partial{z_{f_t}}} = \frac{\partial{loss}}{\partial{c_t}} \cdot \frac{\partial{c_t}}{\partial{f_t}} \cdot \frac{\partial{f_t}}{\partial{z_{f_t}}} \\\\ &= \delta_{c_t} \cdot diag[c_{t-1}] \cdot diag[f_t \circ (1 - f_t)] \\\\ &= \delta_{c_t} \circ c_{t-1} \circ f_t \circ (1 - f_t) \end{aligned} \tag{21}$$

于是，在$t$时刻，输出层参数的各项误差为：

$$d_{W_{o,t}} = \frac{\partial{loss}}{\partial{W_{o,t}}} = \frac{\partial{loss}}{\partial{z_{o_t}}} \cdot \frac{\partial{z_{o_t}}}{\partial{W_o}} = h^{\top}_ {t-1} \cdot \delta_{z_{ot}} \tag{22}$$

$$d_{U_{o,t}} = \frac{\partial{loss}}{\partial{U_{o,t}}} = \frac{\partial{loss}}{\partial{z_{o_t}}} \cdot \frac{\partial{z_{o_t}}}{\partial{U_o}} = x^{\top}_ t \cdot \delta_{z_{ot}} \tag{23}$$

$$d_{b_{o,t}} = \frac{\partial{loss}}{\partial{b_{o,t}}} = \frac{\partial{loss}}{\partial{z_{o_t}}} \cdot \frac{\partial{z_{o_t}}}{\partial{b_o}} = \delta_{z_{ot}} \tag{24}$$

最终误差为各时刻误差之和，则：

$$d_{W_o} = \sum^\tau_{t=1}d_{W_{o,t}} = \sum^\tau_{t=1}h^{\top}_ {t-1} \cdot \delta_{z_{ot}} \tag{25}$$

$$d_{U_o} = \sum^\tau_{t=1}d_{U_{o,t}} = \sum^\tau_{t=1}x^{\top}_ t \cdot \delta_{z_{ot}} \tag{26}$$

$$d_{b_o} = \sum^\tau_{t=1}d_{b_{o,t}} = \sum^\tau_{t=1}\delta_{z_{ot}} \tag{27}$$

同理可得：

$$d_{W_{c}} = \sum^\tau_{t=1}d_{W_{c,t}} = \sum^\tau_{t=1}h^{\top}_ {t-1} \cdot \delta_{z_{\tilde{c}t}} \tag{28}$$

$$d_{U_{c}} = \sum^\tau_{t=1}d_{U_{c,t}} = \sum^\tau_{t=1}x^{\top}_ t \cdot \delta_{z_{\tilde{c}t}} \tag{29}$$

$$d_{b_{c}} = \sum^\tau_{t=1}d_{b_{c,t}} = \sum^\tau_{t=1}\delta_{z_{\tilde{c}t}} \tag{30}$$

$$d_{W_{i}} = \sum^\tau_{t=1}d_{W_{i,t}} = \sum^\tau_{t=1}h^{\top}_ {t-1} \cdot \delta_{z_{it}} \tag{31}$$

$$d_{U_{i}} = \sum^\tau_{t=1}d_{U_{i,t}} = \sum^\tau_{t=1}x^{\top}_ t \cdot \delta_{z_{it}} \tag{32}$$

$$d_{b_{i}} = \sum^\tau_{t=1}d_{b_{i,t}} =\sum^\tau_{t=1}\delta_{z_{it}} \tag{33}$$

$$d_{W_{f}} = \sum^\tau_{t=1}d_{W_{f,t}} = \sum^\tau_{t=1}h^{\top}_ {t-1} \cdot \delta_{z_{ft}} \tag{34}$$

$$d_{U_{f}} = \sum^\tau_{t=1}d_{U_{f,t}} = \sum^\tau_{t=1}x^{\top}_ t \cdot \delta_{z_{ft}} \tag{35}$$

$$d_{b_{f}} = \sum^\tau_{t=1}d_{b_{f,t}} = \sum^\tau_{t=1}\delta_{z_{ft}} \tag{36}$$

当前LSTM cell分别向前一时刻（$t-1$）和下一层（$l-1$）传递误差，公式如下：

沿时间向前传递：

$$\begin{aligned} \delta_{h_{t-1}} = \frac{\partial{loss}}{\partial{h_{t-1}}} &= \frac{\partial{loss}}{\partial{z_{ft}}} \cdot \frac{\partial{z_{ft}}}{\partial{h_{t-1}}} + \frac{\partial{loss}}{\partial{z_{it}}} \cdot \frac{\partial{z_{it}}}{\partial{h_{t-1}}} \\\\ &+ \frac{\partial{loss}}{\partial{z_{\tilde{c}t}}} \cdot \frac{\partial{z_{\tilde{c}t}}}{\partial{h_{t-1}}} + \frac{\partial{loss}}{\partial{z_{ot}}} \cdot \frac{\partial{z_{ot}}}{\partial{h_{t-1}}} \\\\ &= \delta_{z_{ft}} \cdot W_f^{\top} + \delta_{z_{it}} \cdot W_i^{\top} + \delta_{z_{\tilde{c}t}} \cdot W_c^{\top} + \delta_{z_{ot}} \cdot W_o^{\top} \end{aligned} \tag{37}$$

沿层次向下传递：

$$\begin{aligned} \delta_{x_t} = \frac{\partial{loss}}{\partial{x_t}} &= \frac{\partial{loss}}{\partial{z_{ft}}} \cdot \frac{\partial{z_{ft}}}{\partial{x_t}} + \frac{\partial{loss}}{\partial{z_{it}}} \cdot \frac{\partial{z_{it}}}{\partial{x_t}} \\\\ &+ \frac{\partial{loss}}{\partial{z_{\tilde{c}t}}} \cdot \frac{\partial{z_{\tilde{c}t}}}{\partial{x_t}} + \frac{\partial{loss}}{\partial{z_{ot}}} \cdot \frac{\partial{z_{ot}}}{\partial{x_t}} \\\\ &= \delta_{z_{ft}} \cdot U_f^{\top} + \delta_{z_{it}} \cdot U_i^{\top} + \delta_{z_{\tilde{c}t}} \cdot U_c^{\top} + \delta_{z_{ot}} \cdot U_o^{\top} \end{aligned} \tag{38}$$

以上，LSTM反向传播公式推导完毕。