Dataflow Modeling¶

How Brainsmith systematically bridges the semantic gap between ONNX's model-level abstractions and RTL's cycle-accurate streaming implementation.

Introduction¶

ONNX describes neural network computation in terms of complete tensors—a LayerNorm operates on an entire (1, 224, 224, 64) activation map. Hardware executes on bit-streams cycling through circuits—16 INT8 elements processed per clock cycle, streamed over hundreds of cycles.

This semantic gap must be bridged systematically. Without a formal model linking tensor operations to streaming execution, you cannot:

Automatically estimate performance - Calculate cycle counts, throughput, and latency from ONNX graph structure
Generate infrastructure - Derive FIFO depths, width converters, and buffering requirements from tensor shapes
Enable design space exploration - Determine valid parallelization ranges and resource tradeoffs without manual analysis
Compose heterogeneous kernels - Connect elementwise, reduction, and attention operations with different processing patterns

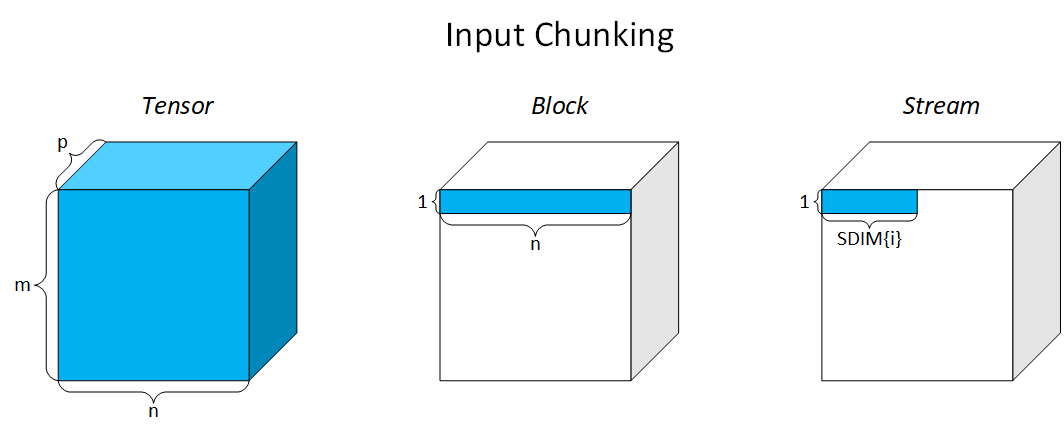
Data Hierarchy: TENSOR/BLOCK/STREAM¶

Brainsmith bridges this gap through a three-tier data hierarchy: TENSOR → BLOCK → STREAM. Each tier refines how data is represented and processed:

TENSOR - Complete dimensions from ONNX graph (e.g., (1, 224, 224, 64))

Defines functional correctness and accuracy requirements
Extracted from ModelWrapper's tensor shape information
Represents the semantic unit of computation from the model

BLOCK - Kernel's atomic computation unit (e.g., (1, 7, 7, 64))

Data required for one cycle of the kernel's computation state
Controls memory footprint, pipeline depth, and latency
Defined by block_tiling template in schema
Determines valid parallelization ranges (STREAM cannot exceed BLOCK)

STREAM - Elements processed per clock cycle (e.g., 16 8-bit Integers)

Determines throughput and resource usage
Defined by stream_tiling template in schema
Constrained by BLOCK shape (cannot exceed block dimensions)
Resolved during DSE configuration (SIMD, PE parameters)

Kernel-Specific Block Semantics¶

The BLOCK abstraction level is necessary because some kernels cannot arbitrarily increase parallelism up to the full TENSOR shape. Consider the following examples, and how the BLOCK shape adapts to kernel computation characteristics:

Simple kernels (elementwise operations like Add, Multiply):

BLOCK = TENSOR (entire input processed as one unit)
No intermediate computation state between elements
STREAM parallelization limited only by resource availability
Example: Add with input (1, 224, 224, 64) → BLOCK (1, 224, 224, 64), STREAM (1, 1, 1, 16)

Complex kernels (reduction operations like MatMul, LayerNorm):

BLOCK = one quantum of the calculation state
Example: Dot product BLOCK = one input vector
Kernel must accumulate/reduce across BLOCK before producing output
STREAM parallelization cannot exceed BLOCK dimensions
Example: LayerNorm with input (1, 224, 224, 64) → BLOCK (1, 1, 1, 64), STREAM (1, 1, 1, 16)

Lowering from ONNX to RTL¶

The streaming data hierarchy enables automatic derivation of hardware execution characteristics:

# Spatial decomposition
tensor_blocks = ceil(tensor_dim / block_dim)

# Temporal execution
stream_cycles = ceil(block_dim / stream_dim)

# Total latency
total_cycles = prod(tensor_blocks) × prod(stream_cycles)

Example: For tensor (100, 64), block (32, 16), stream (8, 4):

Tensor blocks: (4, 4) → 16 blocks cover the full tensor
Stream cycles: (4, 4) → 16 cycles stream each block
Total cycles: 256 (16 blocks × 16 cycles per block)

This calculation forms the basis for: - Performance estimation - Cycle counts and throughput - Resource estimation - Memory requirements from block sizes - DSE constraints - Valid parallelization ranges

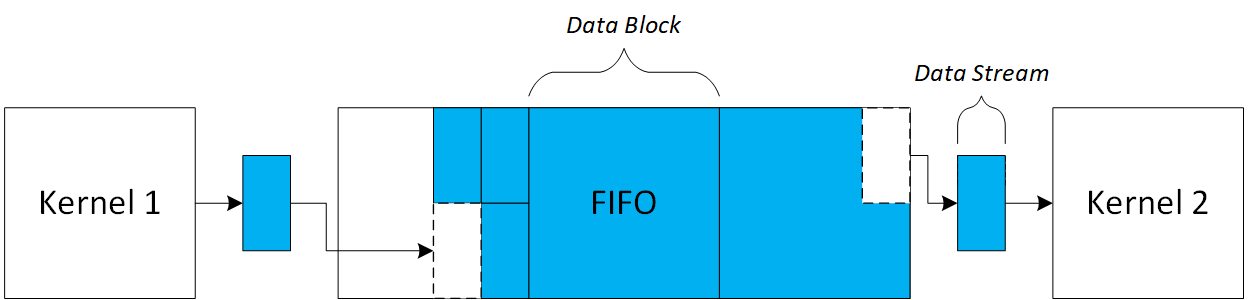
Inter-Kernel Dataflow¶

Kernels communicate via streaming interfaces, producing and consuming data cycle-by-cycle. Elastic FIFOs between kernels accumulate these streams as data blocks for buffering, then stream them out to downstream consumers. This infrastructure automatically adapts to different kernel semantics through shape-driven buffering.

Composing Kernels with Different Block Semantics¶

Consider a simple pipeline: Add → LayerNorm → Softmax

Add (elementwise)           LayerNorm (reduction)       Softmax (reduction)
BLOCK = TENSOR (1,224,64)   BLOCK = (1,1,64)           BLOCK = (1,1,N_classes)
STREAM = (1,1,16)           STREAM = (1,1,16)          STREAM = (1,1,8)

What happens at kernel boundaries:

Add → LayerNorm: Producer outputs (1,224,64) blocks, consumer expects (1,1,64) blocks
FIFO buffers shape transformation
Add streams 14 blocks × 16 cycles each = 224 cycles
LayerNorm consumes in (1,1,64) chunks, computing normalization per spatial position
LayerNorm → Softmax: Block shapes may differ based on computation semantics
Each kernel's BLOCK reflects its reduction domain
FIFOs provide elastic buffering for rate adaptation

Automatic Infrastructure Derivation¶

Block and stream shapes drive hardware generation:

FIFO Depths - Determined by producer/consumer rate mismatch:

producer_rate = prod(block_shape) / prod(stream_shape)  # cycles per block
consumer_rate = # depends on consumer's internal pipeline depth
fifo_depth = max(producer_burst, consumer_backpressure_tolerance)

Implementation Reality

The formula above describes the theoretical basis for FIFO sizing. In practice, the current implementation uses iterative cycle-accurate RTL simulation to converge on efficient FIFO depths. This will be expanded on in future releases.

Stream Width Matching - Interface widths must align:

Producer STREAM=(1,1,16) × INT8 → 128-bit AXI-Stream
Consumer expects matching width or automatic width conversion
Datatype changes (INT8 → FLOAT32) insert conversion logic

Rate Mismatch Handling - Kernels may have different throughputs:

Elementwise: 1 output per cycle (after initial latency)
Reduction: Multiple cycles per output (accumulation phase)
FIFOs absorb transient rate differences, prevent pipeline stalls

Schema-Driven Interface Resolution¶

Schemas declare interfaces using templates that adapt to runtime shapes:

# Producer (Add kernel)
OutputSchema(
    block_tiling=[FULL_DIM, FULL_DIM, FULL_DIM],  # Process entire spatial dims
    stream_tiling=[1, 1, "PE"]                      # Parallelize over channels
)

# Consumer (LayerNorm kernel)
InputSchema(
    block_tiling=[FULL_DIM, FULL_DIM, FULL_DIM],  # Same spatial processing
    stream_tiling=[1, 1, "SIMD"]                    # Match channel parallelism
)

At compile time:

ONNX tensor shapes resolve FULL_DIM → actual dimensions
DSE parameters (PE=16, SIMD=16) resolve stream tiling
Infrastructure generates FIFOs matching computed shapes
Validation ensures producer/consumer compatibility

This declarative approach separates what (tensor semantics) from how (hardware implementation), enabling design space exploration while maintaining correctness by construction. The compiler automatically inserts width converters, reshaping logic, and elastic buffering as needed.

Design Space Implications¶

The dataflow modeling hierarchy directly constrains design space exploration:

Valid Parallelization Ranges:

STREAM dimensions must be divisors of BLOCK dimensions
For BLOCK=(64,), valid STREAM values are {1, 2, 4, 8, 16, 32, 64}
Invalid: STREAM=128 (exceeds block size)

Performance vs Resource Tradeoffs:

Increasing STREAM → Higher throughput, more DSP/LUT usage
Increasing BLOCK → More on-chip memory, potentially higher latency
Heterogeneous pipelines: Balance per-kernel parallelization against total resource budget

Configuration Constraints:

Producer/consumer STREAM widths must match (or have automatic conversion)
Total pipeline throughput limited by slowest kernel
FIFO depths must accommodate worst-case rate mismatches