Skip to contents

Calculate the Lorenz Curve and Gini Coefficient in a Person Query

Source: R/create_lorenz.R
create_lorenz.Rd

This function computes the Gini coefficient and plots the Lorenz curve based on a selected metric from a Person Query data frame. It provides a way to measure inequality in the distribution of the selected metric.This function can be integrated into a larger analysis pipeline to assess inequality in metric distribution.

Usage

create_lorenz(data, metric, return = "plot")

Arguments

data

Data frame containing a Person Query.

metric

Character string identifying the metric to be used for the Lorenz curve and Gini coefficient calculation.

return

Character string identifying the return type. Options are:

  • "gini" - Numeric value representing the Gini coefficient.

  • "table" - Data frame containing a summary table of population share and value share.

  • "plot" (default) - ggplot object representing a plot of the Lorenz curve.

Gini coefficient

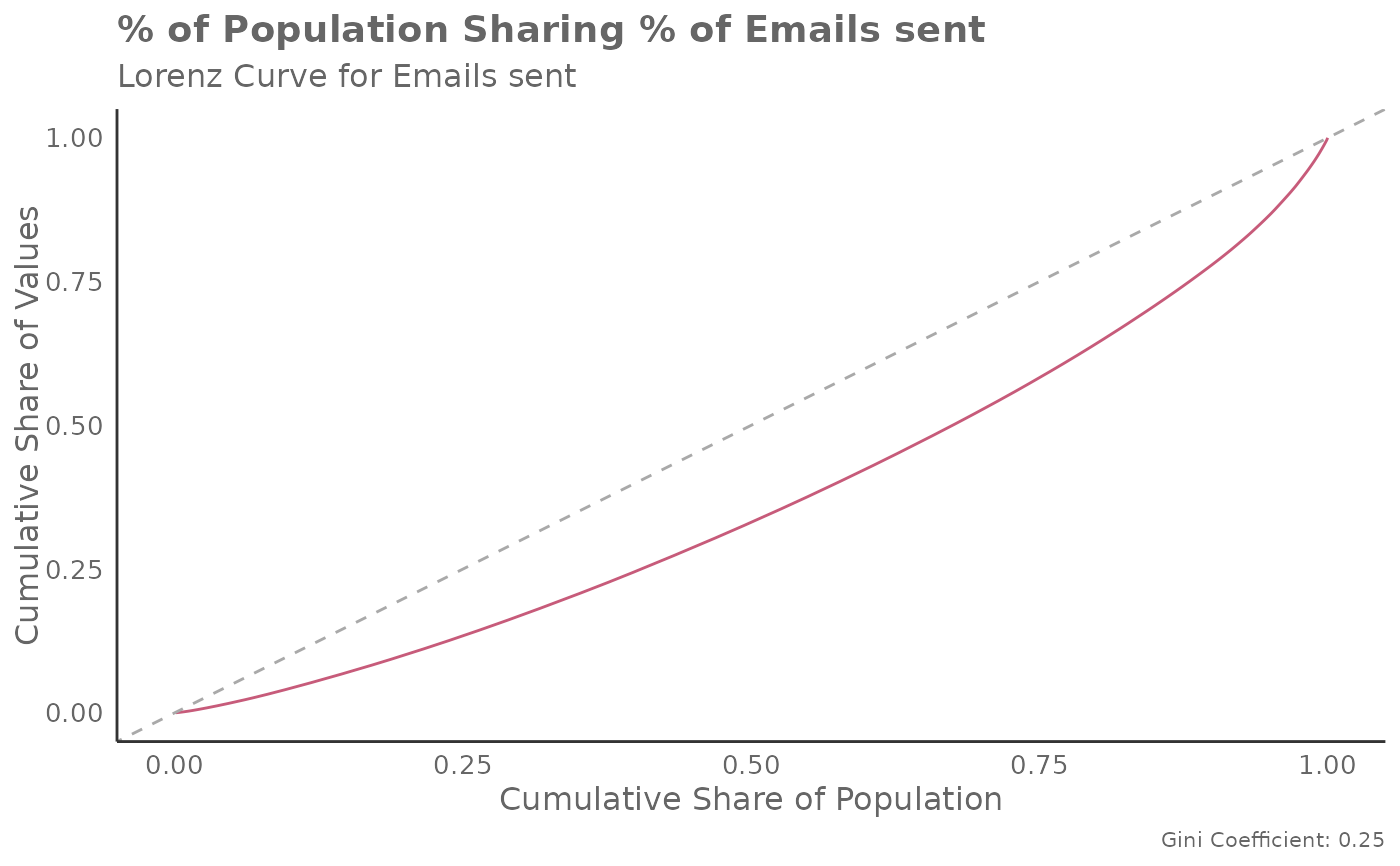
The Gini coefficient is a measure of statistical dispersion most commonly used to represent income inequality within a population. It is calculated as the ratio of the area between the Lorenz curve and the line of perfect equality (the 45-degree line) to the total area under the line of perfect equality. It has a range of 0 to 1, where 0 represents perfect equality and 1 represents perfect inequality. It can be applied to any Viva Insights metric where inequality is of interest.

Examples

create_lorenz(data = pq_data, metric = "Emails_sent", return = "gini")
#> [1] 0.1839071

create_lorenz(data = pq_data, metric = "Emails_sent", return = "plot")


create_lorenz(data = pq_data, metric = "Emails_sent", return = "table")
#> # A tibble: 11 × 2
#>    population_share value_share
#>               <dbl>       <dbl>
#>  1              0    0.00000659
#>  2              0.1  0.0457    
#>  3              0.2  0.112     
#>  4              0.3  0.190     
#>  5              0.4  0.276     
#>  6              0.5  0.370     
#>  7              0.6  0.473     
#>  8              0.7  0.584     
#>  9              0.8  0.706     
#> 10              0.9  0.840     
#> 11              1    1