3 posts tagged with "research"

TL;DR:

• We introduce MathChat, a conversational framework leveraging Large Language Models (LLMs), specifically GPT-4, to solve advanced mathematical problems.
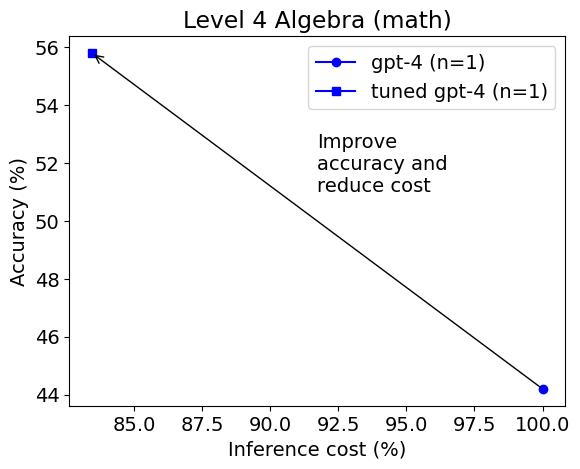
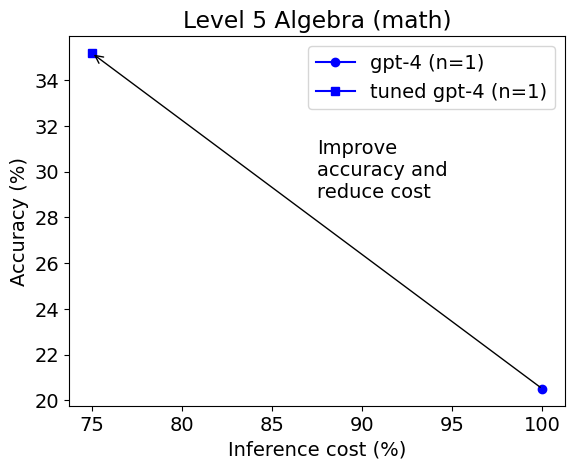
• MathChat improves LLM's performance on challenging math problem-solving, outperforming basic prompting and other strategies by about 6%. The improvement was especially notable in the Algebra category, with a 15% increase in accuracy.
• Despite the advancement, GPT-4 still struggles to solve very challenging math problems, even with effective prompting strategies. Further improvements are needed, such as the development of more specific assistant models or the integration of new tools and prompts.

Recent Large Language Models (LLMs) like GTP-3.5 and GPT-4 have demonstrated astonishing abilities over previous models on various tasks, such as text generation, question answering, and code generation. Moreover, these models can communicate with humans through conversations and remember previous contexts, making it easier for humans to interact with them. These models play an increasingly important role in our daily lives assisting people with different tasks, such as writing emails, summarizing documents, and writing code.

In this blog post, we probe into the problem-solving capabilities of LLMs. Specifically, we are interested in their capabilities to solve advanced math problems, which could be representative of a broader class of problems that require precise reasoning and also have deterministic solutions.

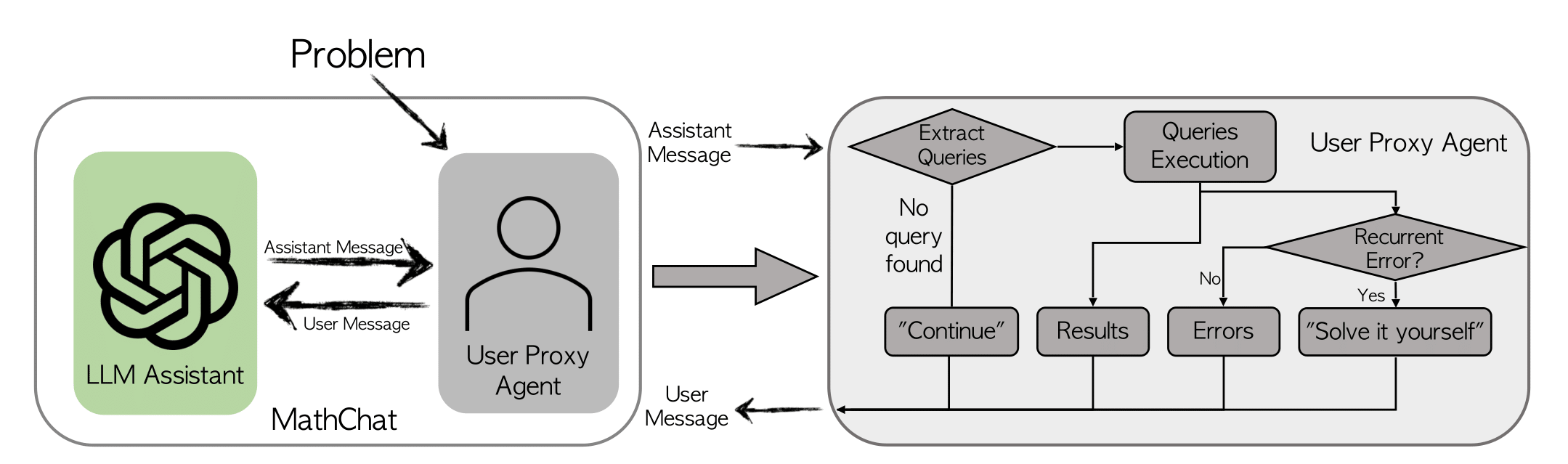
We introduce MathChat, a conversational framework designed for solving challenging math problems with LLMs. This framework takes advantage of the chat-optimized feature of state-of-the-art LLMs, where a user proxy agent and an LLM assistant work together to tackle math problems. We also test previous prompting techniques for comparison.

The MathChat Framework​

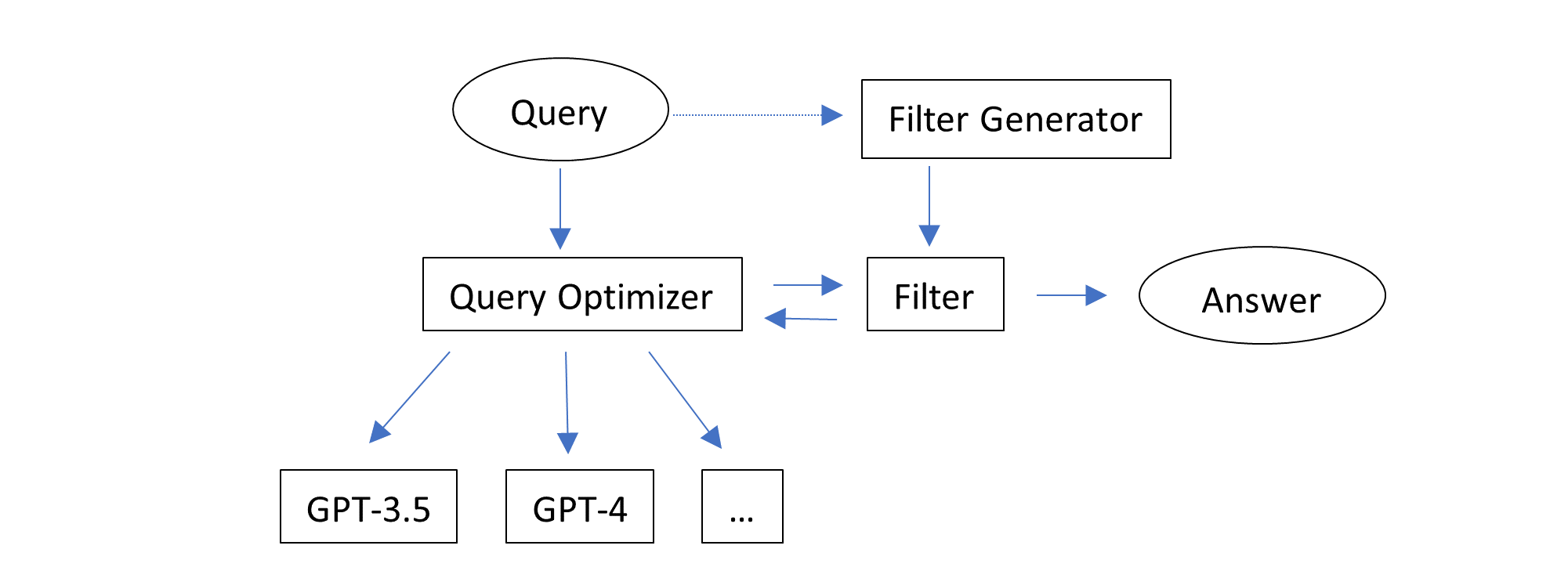
MathChat simulates a conversation between the LLM assistant and a user proxy agent. As the name indicates, the user proxy agent acts as a proxy for the user, which is responsible for communicating with the LLM assistant and continuing the conversation in a desired manner.

The proxy agent first presents a math problem to the LLM assistant, framed by an initial prompt that guides the assistant in how it should work collaboratively to solve the problem. We incorporate existing prompting methods such as CoT (chain-of-thought) and tool-using are incorporated in the initial prompt. Key components of the prompt include:

• Tool-using Prompt: This guides the LLM assistant to use Python code in the correct format to address the problem, allowing the user proxy agent to parse the code and provide the appropriate results.

• Problem-Solving Strategy Selection Prompt: The assistant is instructed to choose one of three potential problem-solving strategies, including:

  1. Writing a Python program to solve the problem directly.
  2. Solving the problem directly without using Python, which exercises LLMs' inherent reasoning capabilities.
  3. Solving the problem step by step with Python. This should be used when the first two strategies aren't suitable.

• Final Answer Encapsulation Prompt: This part instructs the assistant to put the final answer in \boxed{}.

The prompt design in MathChat is flexible and can easily be refined to include other tools, such as Wolfram Alpha.

Let's take a look at an example between the User Proxy Agent and the LLM Assistant (GPT-4). The conversation focuses on how to solve inequality using Python. (The conversation is modified for readability.)

Experiment Setup​

We evaluate the improvement brought by MathChat.

For the experiment, we focus on the level-5 problems from the MATH dataset, which are composed of high school competition problems. These problems include the application of theorems and complex equation derivation and are challenging even for undergraduate students. We evaluate 6 of 7 categories from the dataset (excluding Geometry): Prealgebra, Algebra, Number Theory, Counting and Probability, Intermediate Algebra, and Precalculus.

We evaluate GPT-4 and use the default configuration of the OpenAI API. To access the final performance, we manually compare the final answer with the correct answer. For the vanilla prompt, Program Synthesis, and MathChat, we have GPT-4 enclose the final answer in \boxed{}, and we take the return of the function in PoT as the final answer.

We also evaluate the following methods for comparison:

1. Vanilla prompting: Evaluates GPT-4's direct problem-solving capability. The prompt used is: " Solve the problem carefully. Put the final answer in \boxed{}".

2. Program of Thoughts (PoT): Uses a zero-shot PoT prompt that requests the model to create a Solver function to solve the problem and return the final answer.

3. Program Synthesis (PS) prompting: Like PoT, it prompts the model to write a program to solve the problem. The prompt used is: "Write a program that answers the following question: {Problem}".

Experiment Results​

The accuracy on all the problems with difficulty level-5 from different categories of the MATH dataset with different methods is shown below:

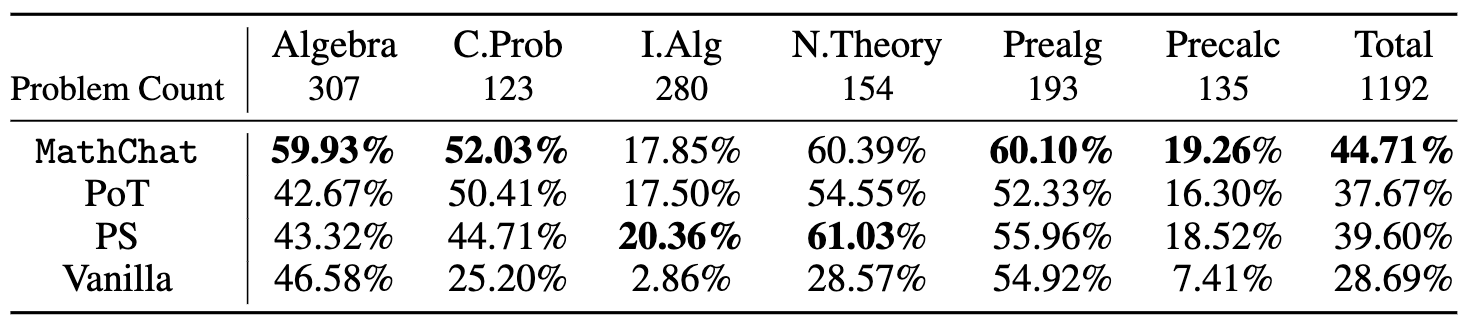
We found that compared to basic prompting, which demonstrates the innate capabilities of GPT-4, utilizing Python within the context of PoT or PS strategy improved the overall accuracy by about 10%. This increase was mostly seen in categories involving more numerical manipulations, such as Counting & Probability and Number Theory, and in more complex categories like Intermediate Algebra and Precalculus.

For categories like Algebra and Prealgebra, PoT and PS showed little improvement, and in some instances, even led to a decrease in accuracy. However, MathChat was able to enhance total accuracy by around 6% compared to PoT and PS, showing competitive performance across all categories. Remarkably, MathChat improved accuracy in the Algebra category by about 15% over other methods. Note that categories like Intermediate Algebra and Precalculus remained challenging for all methods, with only about 20% of problems solved accurately.

The code for experiments can be found at this repository. We now provide an implementation of MathChat using the interactive agents in FLAML. See this notebook for example usage.

Future Directions​

Despite MathChat's improvements over previous methods, the results show that complex math problem is still challenging for recent powerful LLMs, like GPT-4, even with help from external tools.

Further work can be done to enhance this framework or math problem-solving in general:

• Although enabling the model to use tools like Python can reduce calculation errors, LLMs are still prone to logic errors. Methods like self-consistency (Sample several solutions and take a major vote on the final answer), or self-verification (use another LLM instance to check whether an answer is correct) might improve the performance.
• Sometimes, whether the LLM can solve the problem depends on the plan it uses. Some plans require less computation and logical reasoning, leaving less room for mistakes.
• MathChat has the potential to be adapted into a copilot system, which could assist users with math problems. This system could allow users to be more involved in the problem-solving process, potentially enhancing learning.

For Further Reading​

• Research paper of MathChat
• Documentation about flaml.autogen

Are you working on applications that involve math problem-solving? Would you appreciate additional research or support on the application of LLM-based agents for math problem-solving? Please join our Discord server for discussion.

TL;DR:

• A case study using the HumanEval benchmark shows that an adaptive way of using multiple GPT models can achieve both much higher accuracy (from 68% to 90%) and lower inference cost (by 18%) than using GPT-4 for coding.

GPT-4 is a big upgrade of foundation model capability, e.g., in code and math, accompanied by a much higher (more than 10x) price per token to use over GPT-3.5-Turbo. On a code completion benchmark, HumanEval, developed by OpenAI, GPT-4 can successfully solve 68% tasks while GPT-3.5-Turbo does 46%. It is possible to increase the success rate of GPT-4 further by generating multiple responses or making multiple calls. However, that will further increase the cost, which is already nearly 20 times of using GPT-3.5-Turbo and with more restricted API call rate limit. Can we achieve more with less?

In this blog post, we will explore a creative, adaptive way of using GPT models which leads to a big leap forward.

Observations​

• GPT-3.5-Turbo can alrady solve 40%-50% tasks. For these tasks if we never use GPT-4, we can save nearly 40-50% cost.
• If we use the saved cost to generate more responses with GPT-4 for the remaining unsolved tasks, it is possible to solve some more of them while keeping the amortized cost down.

The obstacle of leveraging these observations is that we do not know a priori which tasks can be solved by the cheaper model, which tasks can be solved by the expensive model, and which tasks can be solved by paying even more to the expensive model.

To overcome that obstacle, one may want to predict which task requires what model to solve and how many responses are required for each task. Let's look at one example code completion task:

def vowels_count(s):
    """Write a function vowels_count which takes a string representing
    a word as input and returns the number of vowels in the string.
    Vowels in this case are 'a', 'e', 'i', 'o', 'u'. Here, 'y' is also a
    vowel, but only when it is at the end of the given word.

    Example:
    >>> vowels_count("abcde")
    2
    >>> vowels_count("ACEDY")
    3
    """

Can we predict whether GPT-3.5-Turbo can solve this task or do we need to use GPT-4? My first guess is that GPT-3.5-Turbo can get it right because the instruction is fairly straightforward. Yet, it turns out that GPT-3.5-Turbo does not consistently get it right, if we only give it one chance. It's not obvious (but an interesting research question!) how to predict the performance without actually trying.

What else can we do? We notice that: It's "easier" to verify a given solution than finding a correct solution from scratch.

Some simple example test cases are provided in the docstr. If we already have a response generated by a model, we can use those test cases to filter wrong implementations, and either use a more powerful model or generate more responses, until the result passes the example test cases. Moreover, this step can be automated by asking GPT-3.5-Turbo to generate assertion statements from the examples given in the docstr (a simpler task where we can place our bet) and executing the code.

Solution​

Combining these observations, we can design a solution with two intuitive ideas:

• Make use of auto-generated feedback, i.e., code execution results, to filter responses.
• Try inference configurations one by one, until one response can pass the filter.

This solution works adaptively without knowing or predicting which task fits which configuration. It simply tries multiple configurations one by one, starting from the cheapest configuration. Note that one configuration can generate multiple responses (by setting the inference parameter n larger than 1). And different configurations can use the same model and different inference parameters such as n and temperature. Only one response is returned and evaluated per task.

An implementation of this solution is provided in flaml.autogen. It uses the following sequence of configurations:

1. GPT-3.5-Turbo, n=1, temperature=0
2. GPT-3.5-Turbo, n=7, temperature=1, stop=["\nclass", "\ndef", "\nif", "\nprint"]
3. GPT-4, n=1, temperature=0
4. GPT-4, n=2, temperature=1, stop=["\nclass", "\ndef", "\nif", "\nprint"]
5. GPT-4, n=1, temperature=1, stop=["\nclass", "\ndef", "\nif", "\nprint"]

Experiment Results​

The first figure in this blog post shows the success rate and average inference cost of the adaptive solution compared with default GPT-4. The inference cost includes the cost for generating the assertions in our solution. The generated assertions are not always correct, and programs that pass/fail the generated assertions are not always right/wrong. Despite of that, the adaptive solution can increase the success rate (referred to as pass@1 in the literature) from 68% to 90%, while reducing the cost by 18%.

Here are a few examples of function definitions which are solved by different configurations in the portfolio.

1. Solved by GPT-3.5-Turbo, n=1, temperature=0

def compare(game,guess):
    """I think we all remember that feeling when the result of some long-awaited
    event is finally known. The feelings and thoughts you have at that moment are
    definitely worth noting down and comparing.
    Your task is to determine if a person correctly guessed the results of a number of matches.
    You are given two arrays of scores and guesses of equal length, where each index shows a match.
    Return an array of the same length denoting how far off each guess was. If they have guessed correctly,
    the value is 0, and if not, the value is the absolute difference between the guess and the score.


    example:

    compare([1,2,3,4,5,1],[1,2,3,4,2,-2]) -> [0,0,0,0,3,3]
    compare([0,5,0,0,0,4],[4,1,1,0,0,-2]) -> [4,4,1,0,0,6]
    """

2. Solved by GPT-3.5-Turbo, n=7, temperature=1, stop=["\nclass", "\ndef", "\nif", "\nprint"]: the vowels_count function presented earlier.
3. Solved by GPT-4, n=1, temperature=0:

def string_xor(a: str, b: str) -> str:
    """ Input are two strings a and b consisting only of 1s and 0s.
    Perform binary XOR on these inputs and return result also as a string.
    >>> string_xor('010', '110')
    '100'
    """

4. Solved by GPT-4, n=2, temperature=1, stop=["\nclass", "\ndef", "\nif", "\nprint"]:

def is_palindrome(string: str) -> bool:
    """ Test if given string is a palindrome """
    return string == string[::-1]


def make_palindrome(string: str) -> str:
    """ Find the shortest palindrome that begins with a supplied string.
    Algorithm idea is simple:
    - Find the longest postfix of supplied string that is a palindrome.
    - Append to the end of the string reverse of a string prefix that comes before the palindromic suffix.
    >>> make_palindrome('')
    ''
    >>> make_palindrome('cat')
    'catac'
    >>> make_palindrome('cata')
    'catac'
    """

5. Solved by GPT-4, n=1, temperature=1, stop=["\nclass", "\ndef", "\nif", "\nprint"]:

def sort_array(arr):
    """
    In this Kata, you have to sort an array of non-negative integers according to
    number of ones in their binary representation in ascending order.
    For similar number of ones, sort based on decimal value.

    It must be implemented like this:
    >>> sort_array([1, 5, 2, 3, 4]) == [1, 2, 3, 4, 5]
    >>> sort_array([-2, -3, -4, -5, -6]) == [-6, -5, -4, -3, -2]
    >>> sort_array([1, 0, 2, 3, 4]) [0, 1, 2, 3, 4]
    """

The last problem is an example with wrong example test cases in the original definition. It misleads the adaptive solution because a correct implementation is regarded as wrong and more trials are made. The last configuration in the sequence returns the right implementation, even though it does not pass the auto-generated assertions. This example demonstrates that:

• Our adaptive solution has a certain degree of fault tolerance.
• The success rate and inference cost for the adaptive solution can be further improved if correct example test cases are used.

It is worth noting that the reduced inference cost is the amortized cost over all the tasks. For each individual task, the cost can be either larger or smaller than directly using GPT-4. This is the nature of the adaptive solution: The cost is in general larger for difficult tasks than that for easy tasks.

An example notebook to run this experiment can be found at: https://github.com/microsoft/FLAML/blob/v1.2.1/notebook/research/autogen_code.ipynb

Discussion​

Our solution is quite simple to implement using a generic interface offered in flaml.autogen, yet the result is quite encouraging.

While the specific way of generating assertions is application-specific, the main ideas are general in LLM operations:

• Generate multiple responses to select - especially useful when selecting a good response is relatively easier than generating a good response at one shot.
• Consider multiple configurations to generate responses - especially useful when:
  • Model and other inference parameter choice affect the utility-cost tradeoff; or
  • Different configurations have complementary effect.

A previous blog post provides evidence that these ideas are relevant in solving math problems too. flaml.autogen uses a technique EcoOptiGen to support inference parameter tuning and model selection.

There are many directions of extensions in research and development:

• Generalize the way to provide feedback.
• Automate the process of optimizing the configurations.
• Build adaptive agents for different applications.

Do you find this approach applicable to your use case? Do you have any other challenge to share about LLM applications? Do you like to see more support or research of LLM optimization or automation? Please join our Discord server for discussion.

For Further Reading​

• Documentation about flaml.autogen and Research paper.
• Blog post about a related study for math.

TL;DR:

• Just by tuning the inference parameters like model, number of responses, temperature etc. without changing any model weights or prompt, the baseline accuracy of untuned gpt-4 can be improved by 20% in high school math competition problems.
• For easy problems, the tuned gpt-3.5-turbo model vastly outperformed untuned gpt-4 in accuracy (e.g., 90% vs. 70%) and cost efficiency. For hard problems, the tuned gpt-4 is much more accurate (e.g., 35% vs. 20%) and less expensive than untuned gpt-4.
• FLAML can help with model selection, parameter tuning, and cost-saving in LLM applications.

Large language models (LLMs) are powerful tools that can generate natural language texts for various applications, such as chatbots, summarization, translation, and more. GPT-4 is currently the state of the art LLM in the world. Is model selection irrelevant? What about inference parameters?

In this blog post, we will explore how model and inference parameter matter in LLM applications, using a case study for MATH, a benchmark for evaluating LLMs on advanced mathematical problem solving. MATH consists of 12K math competition problems from AMC-10, AMC-12 and AIME. Each problem is accompanied by a step-by-step solution.

We will use the new subpackage flaml.autogen to automatically find the best model and inference parameter for LLMs on a given task and dataset given an inference budget, using a novel low-cost search & pruning strategy. FLAML currently supports all the LLMs from OpenAI, such as GPT-3.5 and GPT-4.

We will use FLAML to perform model selection and inference parameter tuning. Then we compare the performance and inference cost on solving algebra problems with the untuned gpt-4. We will also analyze how different difficulty levels affect the results.

Experiment Setup​

We use FLAML to select between the following models with a target inference budget $0.02 per instance:

• gpt-3.5-turbo, a relatively cheap model that powers the popular ChatGPT app
• gpt-4, the state of the art LLM that costs more than 10 times of gpt-3.5-turbo

We adapt the models using 20 examples in the train set, using the problem statement as the input and generating the solution as the output. We use the following inference parameters:

• temperature: The parameter that controls the randomness of the output text. A higher temperature means more diversity but less coherence. We search for the optimal temperature in the range of [0, 1].
• top_p: The parameter that controls the probability mass of the output tokens. Only tokens with a cumulative probability less than or equal to top-p are considered. A lower top-p means more diversity but less coherence. We search for the optimal top-p in the range of [0, 1].
• max_tokens: The maximum number of tokens that can be generated for each output. We search for the optimal max length in the range of [50, 1000].
• n: The number of responses to generate. We search for the optimal n in the range of [1, 100].
• prompt: We use the template: "{problem} Solve the problem carefully. Simplify your answer as much as possible. Put the final answer in \boxed{{}}." where {problem} will be replaced by the math problem instance.

In this experiment, when n > 1, we find the answer with highest votes among all the responses and then select it as the final answer to compare with the ground truth. For example, if n = 5 and 3 of the responses contain a final answer 301 while 2 of the responses contain a final answer 159, we choose 301 as the final answer. This can help with resolving potential errors due to randomness. We use the average accuracy and average inference cost as the metric to evaluate the performance over a dataset. The inference cost of a particular instance is measured by the price per 1K tokens and the number of tokens consumed.

Experiment Results​

The first figure in this blog post shows the average accuracy and average inference cost of each configuration on the level 2 Algebra test set.

Surprisingly, the tuned gpt-3.5-turbo model is selected as a better model and it vastly outperforms untuned gpt-4 in accuracy (92% vs. 70%) with equal or 2.5 times higher inference budget. The same observation can be obtained on the level 3 Algebra test set.

However, the selected model changes on level 4 Algebra.

This time gpt-4 is selected as the best model. The tuned gpt-4 achieves much higher accuracy (56% vs. 44%) and lower cost than the untuned gpt-4. On level 5 the result is similar.

We can see that FLAML has found different optimal model and inference parameters for each subset of a particular level, which shows that these parameters matter in cost-sensitive LLM applications and need to be carefully tuned or adapted.

An example notebook to run these experiments can be found at: https://github.com/microsoft/FLAML/blob/v1.2.1/notebook/autogen_chatgpt.ipynb

Analysis and Discussion​

While gpt-3.5-turbo demonstrates competitive accuracy with voted answers in relatively easy algebra problems under the same inference budget, gpt-4 is a better choice for the most difficult problems. In general, through parameter tuning and model selection, we can identify the opportunity to save the expensive model for more challenging tasks, and improve the overall effectiveness of a budget-constrained system.

There are many other alternative ways of solving math problems, which we have not covered in this blog post. When there are choices beyond the inference parameters, they can be generally tuned via flaml.tune.

The need for model selection, parameter tuning and cost saving is not specific to the math problems. The Auto-GPT project is an example where high cost can easily prevent a generic complex task to be accomplished as it needs many LLM inference calls.

For Further Reading​

• Research paper about the tuning technique
• Documentation about flaml.autogen

Do you have any experience to share about LLM applications? Do you like to see more support or research of LLM optimization or automation? Please join our Discord server for discussion.