Tune User Defined Function

flaml.tune is a module for economical hyperparameter tuning. It is used internally by flaml.AutoML. It can also be used to directly tune a user-defined function (UDF), which is not limited to machine learning model training. You can use flaml.tune instead of flaml.AutoML if one of the following is true:

Your machine learning task is not one of the built-in tasks from flaml.AutoML.
Your input cannot be represented as X_train + y_train or dataframe + label.
The optimization metric is not measurable via validation data only. For example, when you want to directly optimize a downstream application instead of a model accuracy metric.
You need to tune a function that may not even be a machine learning procedure.

Basic Tuning Procedure

There are three essential steps (assuming the knowledge of the set of hyperparameters to tune) to use flaml.tune to finish a basic tuning task:

Specify the tuning objective with respect to the hyperparameters.
Specify a search space of the hyperparameters.
Specify tuning constraints, including constraints on the resource budget to do the tuning, constraints on the configurations, or/and constraints on a (or multiple) particular metric(s).

With these steps, you can perform a basic tuning task accordingly.

Tuning objective

Related arguments:

evaluation_function: A user-defined evaluation function.
metric: A string of the metric name to optimize for.
mode: A string in ['min', 'max'] to specify the objective as minimization or maximization.

The first step is to specify your tuning objective. To do it, you should first specify your evaluation procedure (e.g., perform a machine learning model training and validation) with respect to the hyperparameters in a user-defined function evaluation_function. The function requires a hyperparameter configuration as input, and can simply return a metric value in a scalar or return a dictionary of metric name and metric value pairs.

In the following code, we define an evaluation function with respect to two hyperparameters named x and y according to $obj := (x-85000)^2 - x/y$ . Note that we use this toy example here for more accessible demonstration purposes. In real use cases, the evaluation function usually cannot be written in this closed form, but instead involves a black-box and expensive evaluation procedure. Please check out Tune HuggingFace, Tune PyTorch and Tune LightGBM for real examples of tuning tasks.

import time


def evaluate_config(config: dict):
    """evaluate a hyperparameter configuration"""
    score = (config["x"] - 85000) ** 2 - config["x"] / config["y"]
    # usually the evaluation takes an non-neglible cost
    # and the cost could be related to certain hyperparameters
    # here we simulate this cost by calling the time.sleep() function
    # here we assume the cost is proportional to x
    faked_evaluation_cost = config["x"] / 100000
    time.sleep(faked_evaluation_cost)
    # we can return a single float as a score on the input config:
    # return score
    # or, we can return a dictionary that maps metric name to metric value:
    return {
        "score": score,
        "evaluation_cost": faked_evaluation_cost,
        "constraint_metric": config["x"] * config["y"],
    }

When the evaluation function returns a dictionary of metrics, you need to specify the name of the metric to optimize via the argument metric (this can be skipped when the function is just returning a scalar). In addition, you need to specify a mode of your optimization/tuning task (maximization or minimization) via the argument mode by choosing from "min" or "max".

For example,

flaml.tune.run(evaluation_function=evaluate_config, metric="score", mode="min", ...)

Search space

Related arguments:

config: A dictionary to specify the search space.
low_cost_partial_config (optional): A dictionary from a subset of controlled dimensions to the initial low-cost values.
cat_hp_cost (optional): A dictionary from a subset of categorical dimensions to the relative cost of each choice.

The second step is to specify a search space of the hyperparameters through the argument config. In the search space, you need to specify valid values for your hyperparameters and can specify how these values are sampled (e.g., from a uniform distribution or a log-uniform distribution).

In the following code example, we include a search space for the two hyperparameters x and y as introduced above. The valid values for both are integers in the range of [1, 100000]. The values for x are sampled uniformly in the specified range (using tune.randint(lower=1, upper=100000)), and the values for y are sampled uniformly in logarithmic space of the specified range (using tune.lograndit(lower=1, upper=100000)).

from flaml import tune

# construct a search space for the hyperparameters x and y.
config_search_space = {
    "x": tune.lograndint(lower=1, upper=100000),
    "y": tune.randint(lower=1, upper=100000),
}

# provide the search space to tune.run
tune.run(..., config=config_search_space, ...)

Details and guidelines on hyperparameter search space

The corresponding value of a particular hyperparameter in the search space dictionary is called a domain, for example, tune.randint(lower=1, upper=100000) is the domain for the hyperparameter y. The domain specifies a type and valid range to sample parameters from. Supported types include float, integer, and categorical.

Categorical hyperparameter

If it is a categorical hyperparameter, then you should use tune.choice(possible_choices) in which possible_choices is the list of possible categorical values of the hyperparameter. For example, if you are tuning the optimizer used in model training, and the candidate optimizers are "sgd" and "adam", you should specify the search space in the following way:

{
    "optimizer": tune.choice(["sgd", "adam"]),
}

Numerical hyperparameter

If it is a numerical hyperparameter, you need to know whether it takes integer values or float values. In addition, you need to know:

The range of valid values, i.e., what are the lower limit and upper limit of the hyperparameter value?
Do you want to sample in linear scale or log scale? It is a common practice to sample in the log scale if the valid value range is large and the evaluation function changes more regularly with respect to the log domain, as shown in the following example for learning rate tuning. In this code example, we set the lower limit and the upper limit of the learning rate to be 1/1024 and 1.0, respectively. We sample in the log space because model performance changes more regularly in the log scale with respect to the learning rate within such a large search range.

{
    "learning_rate": tune.loguniform(lower=1 / 1024, upper=1.0),
}

When the search range of learning rate is small, it is more common to sample in the linear scale as shown in the following example,

{
    "learning_rate": tune.uniform(lower=0.1, upper=0.2),
}

Do you have quantization granularity requirements?

When you have a desired quantization granularity for the hyperparameter change, you can use tune.qlograndint or tune.qloguniform to realize the quantization requirement. The following code example helps you realize the need for sampling uniformly in the range of 0.1 and 0.2 with increments of 0.02, i.e., the sampled learning rate can only take values in {0.1, 0.12, 0.14, 0.16, ..., 0.2},

{
    "learning_rate": tune.quniform(lower=0.1, upper=0.2, q=0.02),
}

You can find the corresponding search space choice in the table below once you have answers to the aforementioned three questions.

	Integer	Float
linear scale	tune.randint(lower: int, upper: int)	tune.uniform(lower: float, upper: float)
log scale	tune.lograndint(lower: int, upper: int, base: float = 10	tune.loguniform(lower: float, upper: float, base: float = 10)
linear scale with quantization	tune.qrandint(lower: int, upper: int, q: int = 1)	tune.quniform(lower: float, upper: float, q: float = 1)
log scale with quantization	tune.qlograndint(lower: int, upper, q: int = 1, base: float = 10)	tune.qloguniform(lower: float, upper, q: float = 1, base: float = 10)

See the example below for the commonly used types of domains.

config = {
    # Sample a float uniformly between -5.0 and -1.0
    "uniform": tune.uniform(-5, -1),
    # Sample a float uniformly between 3.2 and 5.4,
    # rounding to increments of 0.2
    "quniform": tune.quniform(3.2, 5.4, 0.2),
    # Sample a float uniformly between 0.0001 and 0.01, while
    # sampling in log space
    "loguniform": tune.loguniform(1e-4, 1e-2),
    # Sample a float uniformly between 0.0001 and 0.1, while
    # sampling in log space and rounding to increments of 0.00005
    "qloguniform": tune.qloguniform(1e-4, 1e-1, 5e-5),
    # Sample a random float from a normal distribution with
    # mean=10 and sd=2
    "randn": tune.randn(10, 2),
    # Sample a random float from a normal distribution with
    # mean=10 and sd=2, rounding to increments of 0.2
    "qrandn": tune.qrandn(10, 2, 0.2),
    # Sample a integer uniformly between -9 (inclusive) and 15 (exclusive)
    "randint": tune.randint(-9, 15),
    # Sample a random uniformly between -21 (inclusive) and 12 (inclusive (!))
    # rounding to increments of 3 (includes 12)
    "qrandint": tune.qrandint(-21, 12, 3),
    # Sample a integer uniformly between 1 (inclusive) and 10 (exclusive),
    # while sampling in log space
    "lograndint": tune.lograndint(1, 10),
    # Sample a integer uniformly between 2 (inclusive) and 10 (inclusive (!)),
    # while sampling in log space and rounding to increments of 2
    "qlograndint": tune.qlograndint(2, 10, 2),
    # Sample an option uniformly from the specified choices
    "choice": tune.choice(["a", "b", "c"]),
}

Cost-related hyperparameters are a subset of the hyperparameters which directly affect the computation cost incurred in the evaluation of any hyperparameter configuration. For example, the number of estimators (n_estimators) and the maximum number of leaves (max_leaves) are known to affect the training cost of tree-based learners. So they are cost-related hyperparameters for tree-based learners.

When cost-related hyperparameters exist, the evaluation cost in the search space is heterogeneous. In this case, designing a search space with proper ranges of the hyperparameter values is highly non-trivial. Classical tuning algorithms such as Bayesian optimization and random search are typically sensitive to such ranges. It may take them a very high cost to find a good choice if the ranges are too large. And if the ranges are too small, the optimal choice(s) may not be included and thus not possible to be found. With our method, you can use a search space with larger ranges in the case of heterogeneous cost.

Our search algorithms are designed to finish the tuning process at a low total cost when the evaluation cost in the search space is heterogeneous. So in such scenarios, if you are aware of low-cost configurations for the cost-related hyperparameters, you are encouraged to set them as the low_cost_partial_config, which is a dictionary of a subset of the hyperparameter coordinates whose value corresponds to a configuration with known low cost. Using the example of the tree-based methods again, since we know that small n_estimators and max_leaves generally correspond to simpler models and thus lower cost, we set {'n_estimators': 4, 'max_leaves': 4} as the low_cost_partial_config by default (note that 4 is the lower bound of search space for these two hyperparameters), e.g., in LGBM. Please find more details on how the algorithm works here.

In addition, if you are aware of the cost relationship between different categorical hyperparameter choices, you are encouraged to provide this information through cat_hp_cost. It also helps the search algorithm to reduce the total cost.

Tuning constraints

Related arguments:

time_budget_s: The time budget in seconds.
num_samples: An integer of the number of configs to try.
config_constraints (optional): A list of config constraints to be satisfied.
metric_constraints (optional): A list of metric constraints to be satisfied. e.g., ['precision', '>=', 0.9].

The third step is to specify constraints of the tuning task. One notable property of flaml.tune is that it is able to finish the tuning process (obtaining good results) within a required resource constraint. A user can either provide the resource constraint in terms of wall-clock time (in seconds) through the argument time_budget_s, or in terms of the number of trials through the argument num_samples. The following example shows three use cases:

# Set a resource constraint of 60 seconds wall-clock time for the tuning.
flaml.tune.run(..., time_budget_s=60, ...)

# Set a resource constraint of 100 trials for the tuning.
flaml.tune.run(..., num_samples=100, ...)

# Use at most 60 seconds and at most 100 trials for the tuning.
flaml.tune.run(..., time_budget_s=60, num_samples=100, ...)

Optionally, you can provide a list of config constraints to be satisfied through the argument config_constraints and provide a list of metric constraints to be satisfied through the argument metric_constraints. We provide more details about related use cases in the Advanced Tuning Options section.

Put together

After the aforementioned key steps, one is ready to perform a tuning task by calling flaml.tune.run(). Below is a quick sequential tuning example using the pre-defined search space config_search_space and a minimization (mode='min') objective for the score metric evaluated in evaluate_config, using the default serach algorithm in flaml. The time budget is 10 seconds (time_budget_s=10).

# require: pip install flaml[blendsearch]
analysis = tune.run(
    evaluate_config,  # the function to evaluate a config
    config=config_search_space,  # the search space defined
    metric="score",
    mode="min",  # the optimization mode, "min" or "max"
    num_samples=-1,  # the maximal number of configs to try, -1 means infinite
    time_budget_s=10,  # the time budget in seconds
)

Result analysis

Once the tuning process finishes, it returns an ExperimentAnalysis object, which provides methods to analyze the tuning.

In the following code example, we retrieve the best configuration found during the tuning, and retrieve the best trial's result from the returned analysis.

analysis = tune.run(
    evaluate_config,  # the function to evaluate a config
    config=config_search_space,  # the search space defined
    metric="score",
    mode="min",  # the optimization mode, "min" or "max"
    num_samples=-1,  # the maximal number of configs to try, -1 means infinite
    time_budget_s=10,  # the time budget in seconds
)
print(analysis.best_config)  # the best config
print(analysis.best_trial.last_result)  # the best trial's result

Advanced Tuning Options

There are several advanced tuning options worth mentioning.

More constraints on the tuning

A user can specify constraints on the configurations to be satisfied via the argument config_constraints. The config_constraints receives a list of such constraints to be satisfied. Specifically, each constraint is a tuple that consists of (1) a function that takes a configuration as input and returns a numerical value; (2) an operation chosen from "\<=", ">=", "\<" or ">"; (3) a numerical threshold.

In the following code example, we constrain the output of area, which takes a configuration as input and outputs a numerical value, to be no larger than 1000.

def my_model_size(config):
    return config["n_estimators"] * config["max_leaves"]


analysis = tune.run(
    ...,
    config_constraints=[(my_model_size, "<=", 40)],
)

You can also specify a list of metric constraints to be satisfied via the argument metric_constraints. Each element in the metric_constraints list is a tuple that consists of (1) a string specifying the name of the metric (the metric name must be defined and returned in the user-defined evaluation_function); (2) an operation chosen from "\<=" or ">="; (3) a numerical threshold.

In the following code example, we constrain the metric training_cost to be no larger than 1 second.

analysis = (tune.run(..., metric_constraints=[("training_cost", "<=", 1)]),)

`config_constraints` vs `metric_constraints`:

The key difference between these two types of constraints is that the calculation of constraints in config_constraints does not rely on the computation procedure in the evaluation function, i.e., in evaluation_function. For example, when a constraint only depends on the config itself, as shown in the code example. Due to this independency, constraints in config_constraints will be checked before evaluation. So configurations that do not satisfy config_constraints will not be evaluated.

Parallel tuning

Related arguments:

use_ray: A boolean of whether to use ray as the backend.
use_spark: A boolean of whether to use spark as the backend.
resources_per_trial: A dictionary of the hardware resources to allocate per trial, e.g., {'cpu': 1}. Only valid when using ray backend.

Details about parallel tuning with Spark could be found here.

You can perform parallel tuning by specifying use_ray=True (requiring flaml[ray] option installed) or use_spark=True (requiring flaml[spark] option installed). You can also limit the amount of resources allocated per trial by specifying resources_per_trial, e.g., resources_per_trial={'cpu': 2} when use_ray=True.

# require: pip install flaml[ray]
analysis = tune.run(
    evaluate_config,  # the function to evaluate a config
    config=config_search_space,  # the search space defined
    metric="score",
    mode="min",  # the optimization mode, "min" or "max"
    num_samples=-1,  # the maximal number of configs to try, -1 means infinite
    time_budget_s=10,  # the time budget in seconds
    use_ray=True,
    resources_per_trial={"cpu": 2},  # limit resources allocated per trial
)
print(analysis.best_trial.last_result)  # the best trial's result
print(analysis.best_config)  # the best config

# require: pip install flaml[spark]
analysis = tune.run(
    evaluate_config,  # the function to evaluate a config
    config=config_search_space,  # the search space defined
    metric="score",
    mode="min",  # the optimization mode, "min" or "max"
    num_samples=-1,  # the maximal number of configs to try, -1 means infinite
    time_budget_s=10,  # the time budget in seconds
    use_spark=True,
)
print(analysis.best_trial.last_result)  # the best trial's result
print(analysis.best_config)  # the best config

A headsup about computation overhead. When parallel tuning is used, there will be a certain amount of computation overhead in each trial. In case each trial's original cost is much smaller than the overhead, parallel tuning can underperform sequential tuning. Sequential tuning is recommended when compute resource is limited, and each trial can consume all the resources.

Trial scheduling

Related arguments:

scheduler: A scheduler for executing the trials.
resource_attr: A string to specify the resource dimension used by the scheduler.
min_resource: A float of the minimal resource to use for the resource_attr.
max_resource: A float of the maximal resource to use for the resource_attr.
reduction_factor: A float of the reduction factor used for incremental pruning.

A scheduler can help manage the trials' execution. It can be used to perform multi-fiedlity evalution, or/and early stopping. You can use two different types of schedulers in flaml.tune via scheduler.

1. An authentic scheduler implemented in FLAML (`scheduler='flaml'`).

This scheduler is authentic to the new search algorithms provided by FLAML. In a nutshell, it starts the search with the minimum resource. It switches between HPO with the current resource and increasing the resource for evaluation depending on which leads to faster improvement.

If this scheduler is used, you need to

Specify a resource dimension. Conceptually a 'resource dimension' is a factor that affects the cost of the evaluation (e.g., sample size, the number of epochs). You need to specify the name of the resource dimension via resource_attr. For example, if resource_attr="sample_size", then the config dict passed to the evaluation_function would contain a key "sample_size" and its value suggested by the search algorithm. That value should be used in the evaluation function to control the compute cost. The larger is the value, the more expensive the evaluation is.
Provide the lower and upper limit of the resource dimension via min_resource and max_resource, and optionally provide reduction_factor, which determines the magnitude of resource (multiplicative) increase when we decide to increase the resource.

In the following code example, we consider the sample size as the resource dimension. It determines how much data is used to perform training as reflected in the evaluation_function. We set the min_resource and max_resource to 1000 and the size of the full training dataset, respectively.

from flaml import tune
from functools import partial
from flaml.automl.data import load_openml_task


def obj_from_resource_attr(resource_attr, X_train, X_test, y_train, y_test, config):
    from lightgbm import LGBMClassifier
    from sklearn.metrics import accuracy_score

    # in this example sample size is our resource dimension
    resource = int(config[resource_attr])
    sampled_X_train = X_train.iloc[:resource]
    sampled_y_train = y_train[:resource]

    # construct a LGBM model from the config
    # note that you need to first remove the resource_attr field
    # from the config as it is not part of the original search space
    model_config = config.copy()
    del model_config[resource_attr]
    model = LGBMClassifier(**model_config)

    model.fit(sampled_X_train, sampled_y_train)
    y_test_predict = model.predict(X_test)
    test_loss = 1.0 - accuracy_score(y_test, y_test_predict)
    return {resource_attr: resource, "loss": test_loss}


X_train, X_test, y_train, y_test = load_openml_task(task_id=7592, data_dir="test/")
max_resource = len(y_train)
resource_attr = "sample_size"
min_resource = 1000
analysis = tune.run(
    partial(obj_from_resource_attr, resource_attr, X_train, X_test, y_train, y_test),
    config={
        "n_estimators": tune.lograndint(lower=4, upper=32768),
        "max_leaves": tune.lograndint(lower=4, upper=32768),
        "learning_rate": tune.loguniform(lower=1 / 1024, upper=1.0),
    },
    metric="loss",
    mode="min",
    resource_attr=resource_attr,
    scheduler="flaml",
    max_resource=max_resource,
    min_resource=min_resource,
    reduction_factor=2,
    time_budget_s=10,
    num_samples=-1,
)

You can find more details about this scheduler in this paper.

2. A scheduler of the `TrialScheduler` class from `ray.tune`.

There is a handful of schedulers of this type implemented in ray.tune, for example, ASHA, HyperBand, BOHB, etc.

To use this type of scheduler you can either (1) set scheduler='asha', which will automatically create an ASHAScheduler instance using the provided inputs (resource_attr, min_resource, max_resource, and reduction_factor); or (2) create an instance by yourself and provided it via scheduler, as shown in the following code example,

#  require: pip install flaml[ray]
from ray.tune.schedulers import HyperBandScheduler
my_scheduler = HyperBandScheduler(time_attr="sample_size", max_t=max_resource, reduction_factor=2)
tune.run(.., scheduler=my_scheduler, ...)

Similar to the case where the flaml scheduler is used, you need to specify the resource dimension, use the resource dimension accordingly in your evaluation_function, and provide the necessary information needed for scheduling, such as min_resource, max_resource and reduction_factor (depending on the requirements of the specific scheduler).
Different from the case when the flaml scheduler is used, the amount of resources to use at each iteration is not suggested by the search algorithm through the resource_attr in a configuration. You need to specify the evaluation schedule explicitly by yourself in the evaluation_function and report intermediate results (using tune.report()) accordingly. In the following code example, we use the ASHA scheduler by setting scheduler="asha". We specify resource_attr, min_resource, min_resource and reduction_factor the same way as in the previous example (when "flaml" is used as the scheduler). We perform the evaluation in a customized schedule.
Use ray backend or not? You can choose to use ray backend or not by specifying use_ray=True or use_ray=False. When ray backend is not used, i.e., use_ray=False, you also need to stop the evaluation function by explicitly catching the StopIteration exception, as shown in the end of the evaluation function obj_w_intermediate_report() in the following code example.

def obj_w_intermediate_report(
    resource_attr, X_train, X_test, y_train, y_test, min_resource, max_resource, config
):
    from lightgbm import LGBMClassifier
    from sklearn.metrics import accuracy_score

    # a customized schedule to perform the evaluation
    eval_schedule = [res for res in range(min_resource, max_resource, 5000)] + [
        max_resource
    ]
    for resource in eval_schedule:
        sampled_X_train = X_train.iloc[:resource]
        sampled_y_train = y_train[:resource]

        # construct a LGBM model from the config
        model = LGBMClassifier(**config)

        model.fit(sampled_X_train, sampled_y_train)
        y_test_predict = model.predict(X_test)
        test_loss = 1.0 - accuracy_score(y_test, y_test_predict)
        # need to report the resource attribute used and the corresponding intermediate results
        try:
            tune.report(sample_size=resource, loss=test_loss)
        except (StopIteration, SystemExit):
            # do cleanup operation here
            return


resource_attr = "sample_size"
min_resource = 1000
max_resource = len(y_train)
analysis = tune.run(
    partial(
        obj_w_intermediate_report,
        resource_attr,
        X_train,
        X_test,
        y_train,
        y_test,
        min_resource,
        max_resource,
    ),
    config={
        "n_estimators": tune.lograndint(lower=4, upper=32768),
        "learning_rate": tune.loguniform(lower=1 / 1024, upper=1.0),
    },
    metric="loss",
    mode="min",
    resource_attr=resource_attr,
    scheduler="asha",
    max_resource=max_resource,
    min_resource=min_resource,
    reduction_factor=2,
    time_budget_s=10,
    num_samples=-1,
)

If you would like to do some cleanup opearation when the trial is stopped by the scheduler, you can do it when you catch the StopIteration (when not using ray) or SystemExit (when using ray) exception explicitly.

Warm start

Related arguments:

points_to_evaluate: A list of initial hyperparameter configurations to run first.
evaluated_rewards: If you have previously evaluated the parameters passed in as points_to_evaluate , you can avoid re-running those trials by passing in the reward attributes as a list so the optimizer can be told the results without needing to re-compute the trial. Must be the same length or shorter length than points_to_evaluate.

If you are aware of some good hyperparameter configurations, you are encouraged to provide them via points_to_evaluate. The search algorithm will try them first and use them to bootstrap the search.

You can use previously evaluated configurations to warm-start your tuning. For example, the following code means that you know the reward for the two configs in points_to_evaluate are 3.99 and 1.99, respectively, and want to inform tune.run().

def simple_obj(config):
    return config["a"] + config["b"]


from flaml import tune

config_search_space = {
    "a": tune.uniform(lower=0, upper=0.99),
    "b": tune.uniform(lower=0, upper=3),
}

points_to_evaluate = [
    {"b": 0.99, "a": 3},
    {"b": 0.99, "a": 2},
    {"b": 0.80, "a": 3},
    {"b": 0.80, "a": 2},
]
evaluated_rewards = [3.99, 2.99]

analysis = tune.run(
    simple_obj,
    config=config_search_space,
    mode="max",
    points_to_evaluate=points_to_evaluate,
    evaluated_rewards=evaluated_rewards,
    time_budget_s=10,
    num_samples=-1,
)

Reproducibility

By default, there is randomness in our tuning process (for versions \<= 0.9.1). If reproducibility is desired, you could manually set a random seed before calling tune.run(). For example, in the following code, we call np.random.seed(100) to set the random seed. With this random seed, running the following code multiple times will generate exactly the same search trajectory. The reproducibility can only be guaranteed in sequential tuning.

import numpy as np

np.random.seed(100)  # This line is not needed starting from version v0.9.2.
analysis = tune.run(
    simple_obj,
    config=config_search_space,
    mode="max",
    num_samples=10,
)

Lexicographic Objectives

We support tuning multiple objectives with lexicographic preference by providing argument lexico_objectives for tune.run(). lexico_objectives is a dictionary that contains the following fields of key-value pairs:

metrics: a list of optimization objectives with the orders reflecting the priorities/preferences of the objectives.
modes: (optional) a list of optimization modes (each mode either "min" or "max") corresponding to the objectives in the metric list. If not provided, we use "min" as the default mode for all the objectives.
tolerances: (optional) a dictionary to specify the optimality tolerances on objectives. The keys are the metric names (provided in "metrics"), and the values are the absolute/percentage tolerance in the form of numeric/string.
targets: (optional) a dictionary to specify the optimization targets on the objectives. The keys are the metric names (provided in "metric"), and the values are the numerical target values.

In the following example, we want to minimize val_loss and pred_time of the model where val_loss has high priority. The tolerances for val_loss and pre_time are 0.02 and 0 respectively. We do not set targets for these two objectives and we set them to -inf for both objectives.

lexico_objectives = {}
lexico_objectives["metrics"] = ["val_loss", "pred_time"]
lexico_objectives["modes"] = ["min", "min"]
lexico_objectives["tolerances"] = {"val_loss": 0.02, "pred_time": 0.0}
lexico_objectives["targets"] = {"val_loss": -float("inf"), "pred_time": -float("inf")}

# provide the lexico_objectives to tune.run
tune.run(..., search_alg=None, lexico_objectives=lexico_objectives)

We also supports providing percentage tolerance as shown below.

lexico_objectives["tolerances"] = {"val_loss": "10%", "pred_time": "0%"}

NOTE:

When lexico_objectives is not None, the arguments metric, mode, will be invalid, and flaml's tune uses CFO as the search_alg, which makes the input (if provided) search_alg invalid.
This is a new feature that will be released in version 1.1.0 and is subject to change in the future version.

Hyperparameter Optimization Algorithm

To tune the hyperparameters toward your objective, you will want to use a hyperparameter optimization algorithm which can help suggest hyperparameters with better performance (regarding your objective). flaml offers two HPO methods: CFO and BlendSearch. flaml.tune uses BlendSearch by default when the option [blendsearch] is installed.

CFO uses the randomized direct search method FLOW² with adaptive stepsize and random restart. It requires a low-cost initial point as input if such point exists. The search begins with the low-cost initial point and gradually move to high cost region if needed. The local search method has a provable convergence rate and bounded cost.

About FLOW²: FLOW² is a simple yet effective randomized direct search method. It is an iterative optimization method that can optimize for black-box functions. FLOW² only requires pairwise comparisons between function values to perform iterative update. Comparing to existing HPO methods, FLOW² has the following appealing properties:

It is applicable to general black-box functions with a good convergence rate in terms of loss.
It provides theoretical guarantees on the total evaluation cost incurred.

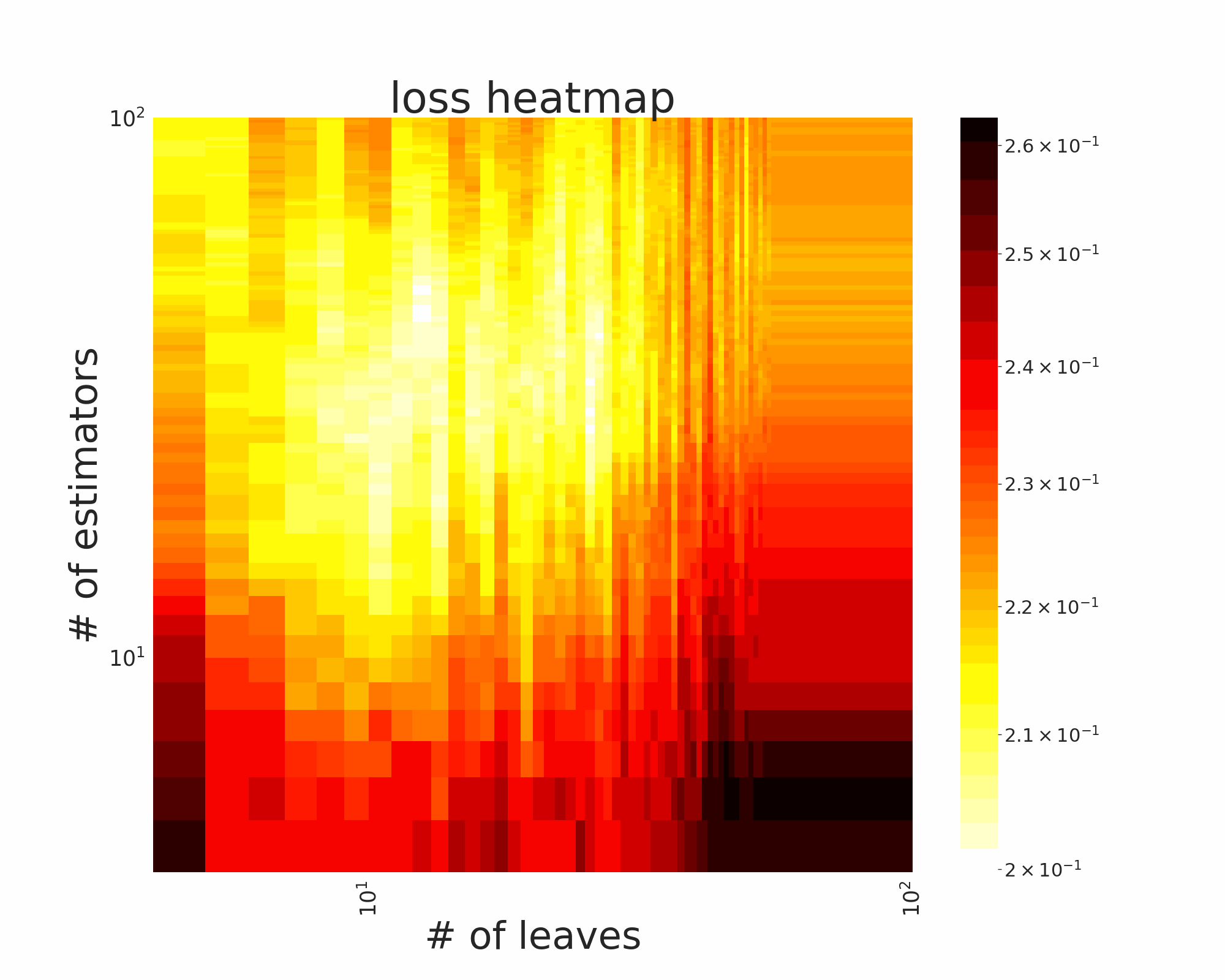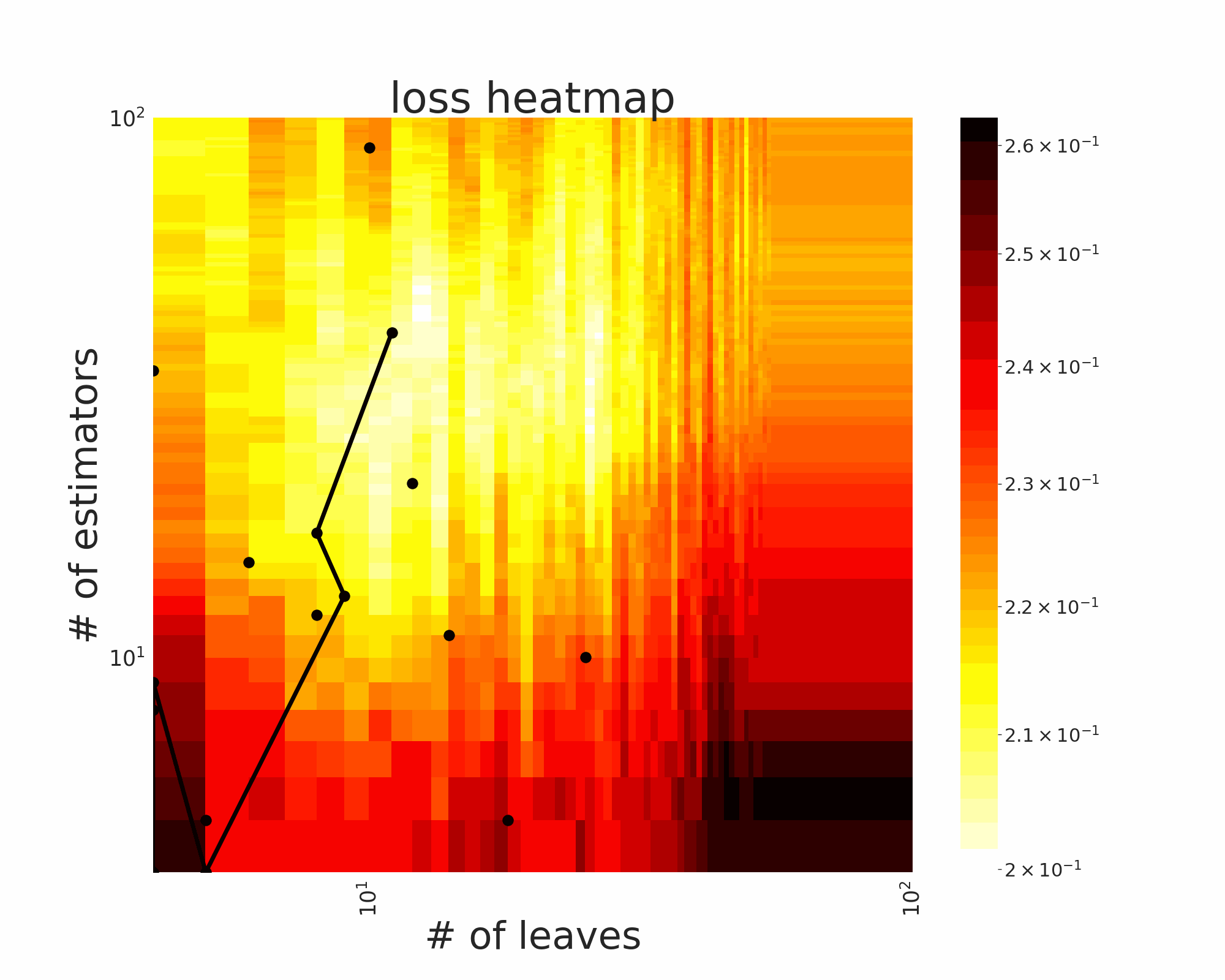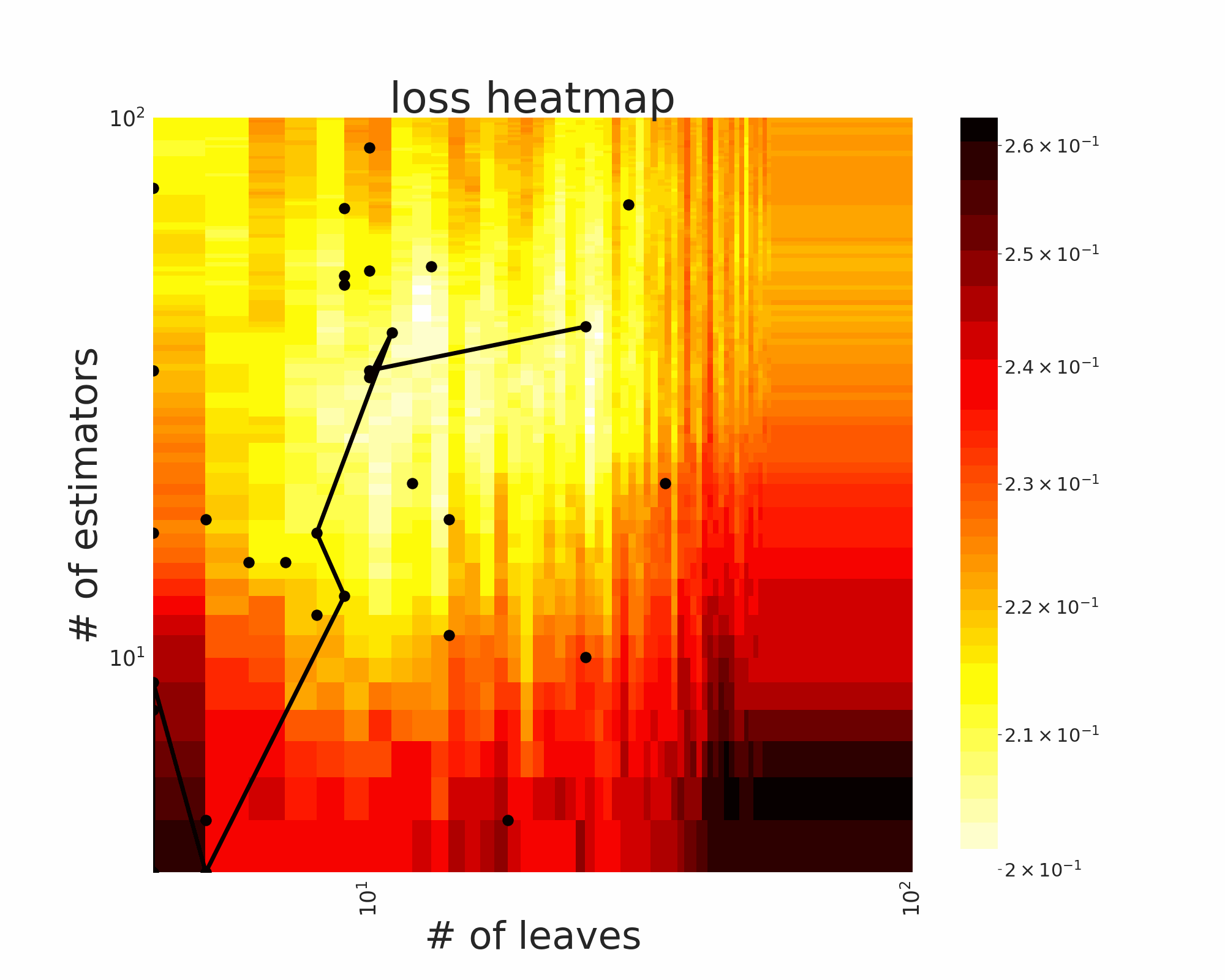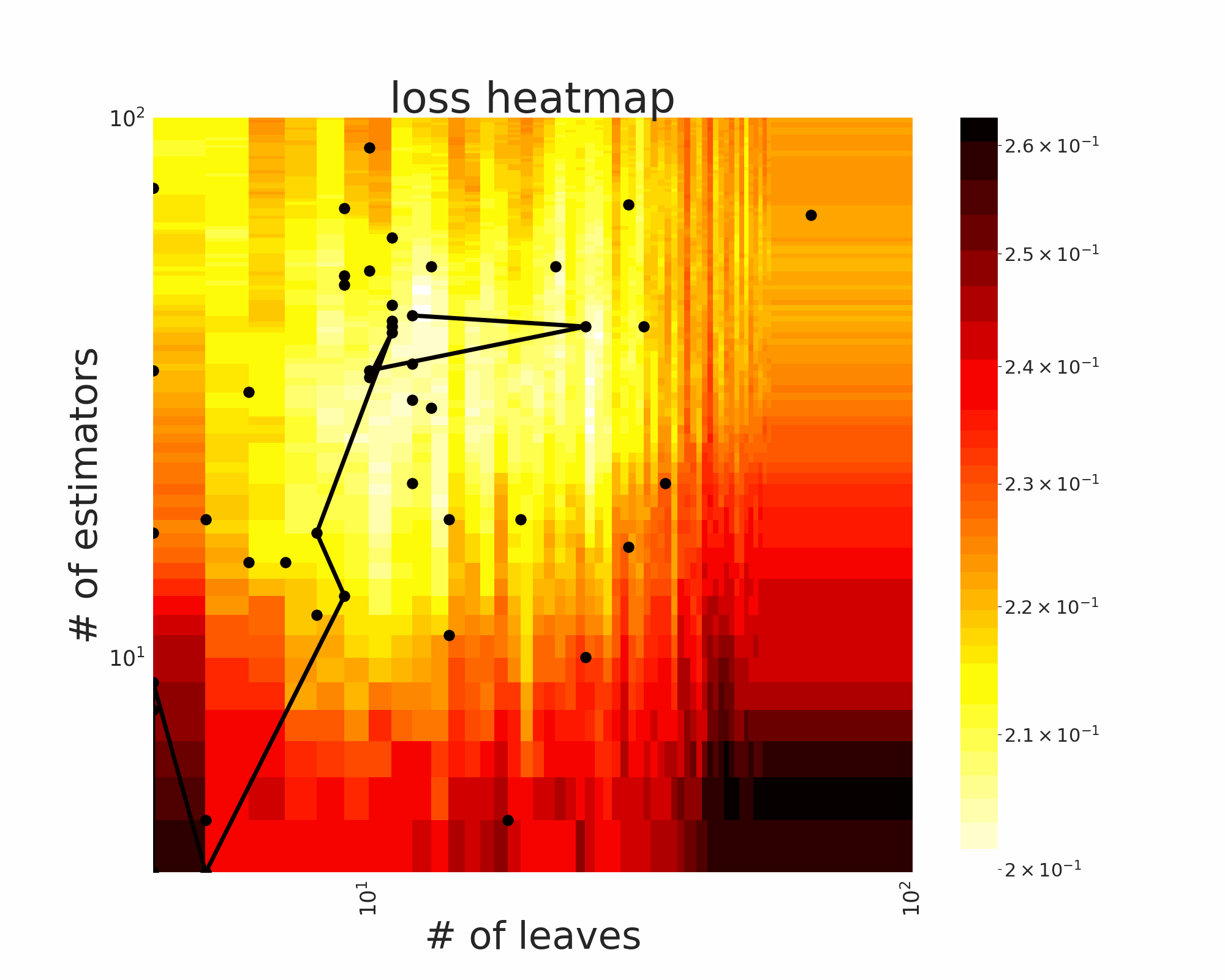
The GIFs attached below demonstrate an example search trajectory of FLOW² shown in the loss and evaluation cost (i.e., the training time ) space respectively. FLOW² is used in tuning the # of leaves and the # of trees for XGBoost. The two background heatmaps show the loss and cost distribution of all configurations. The black dots are the points evaluated in FLOW². Black dots connected by lines are points that yield better loss performance when evaluated.

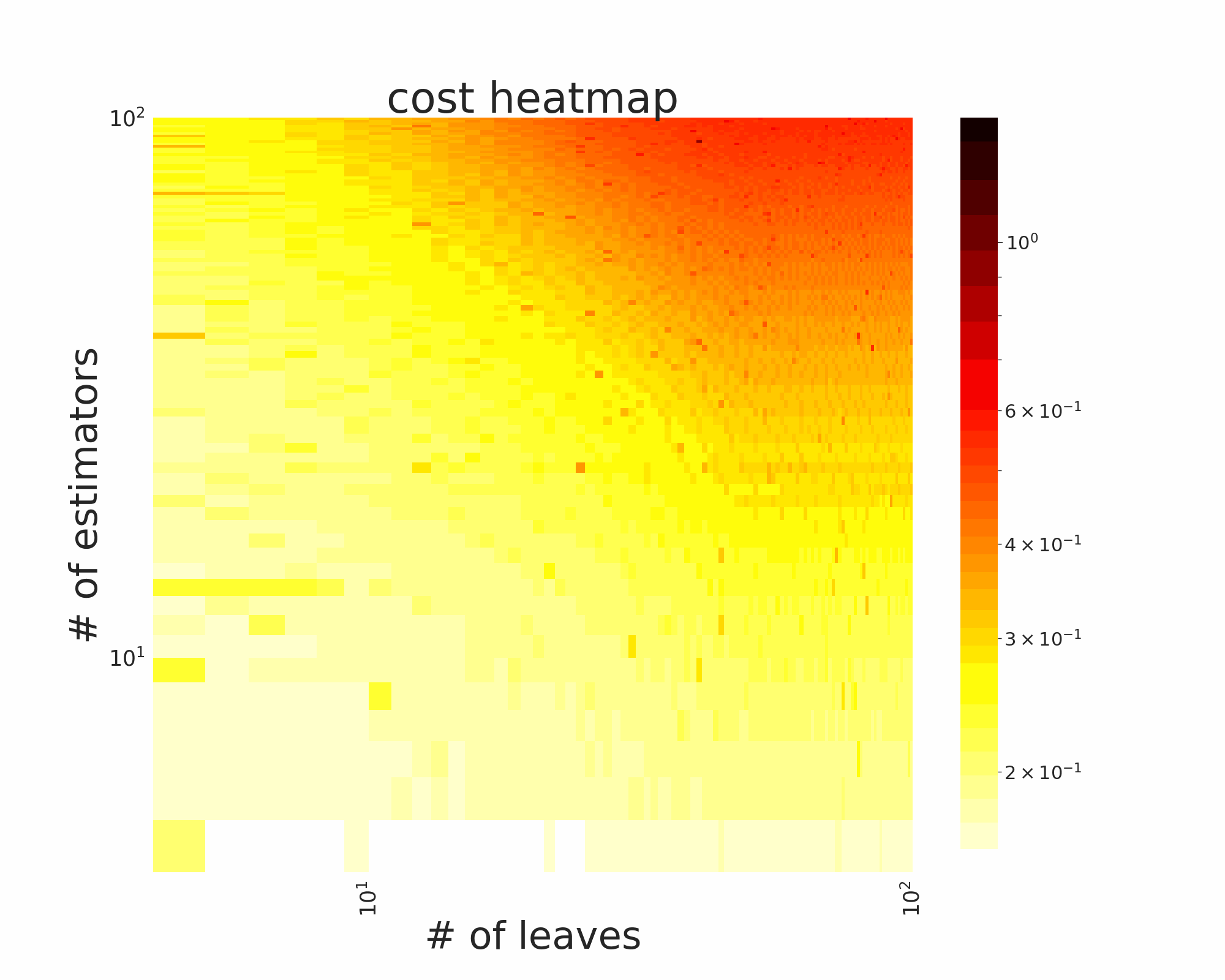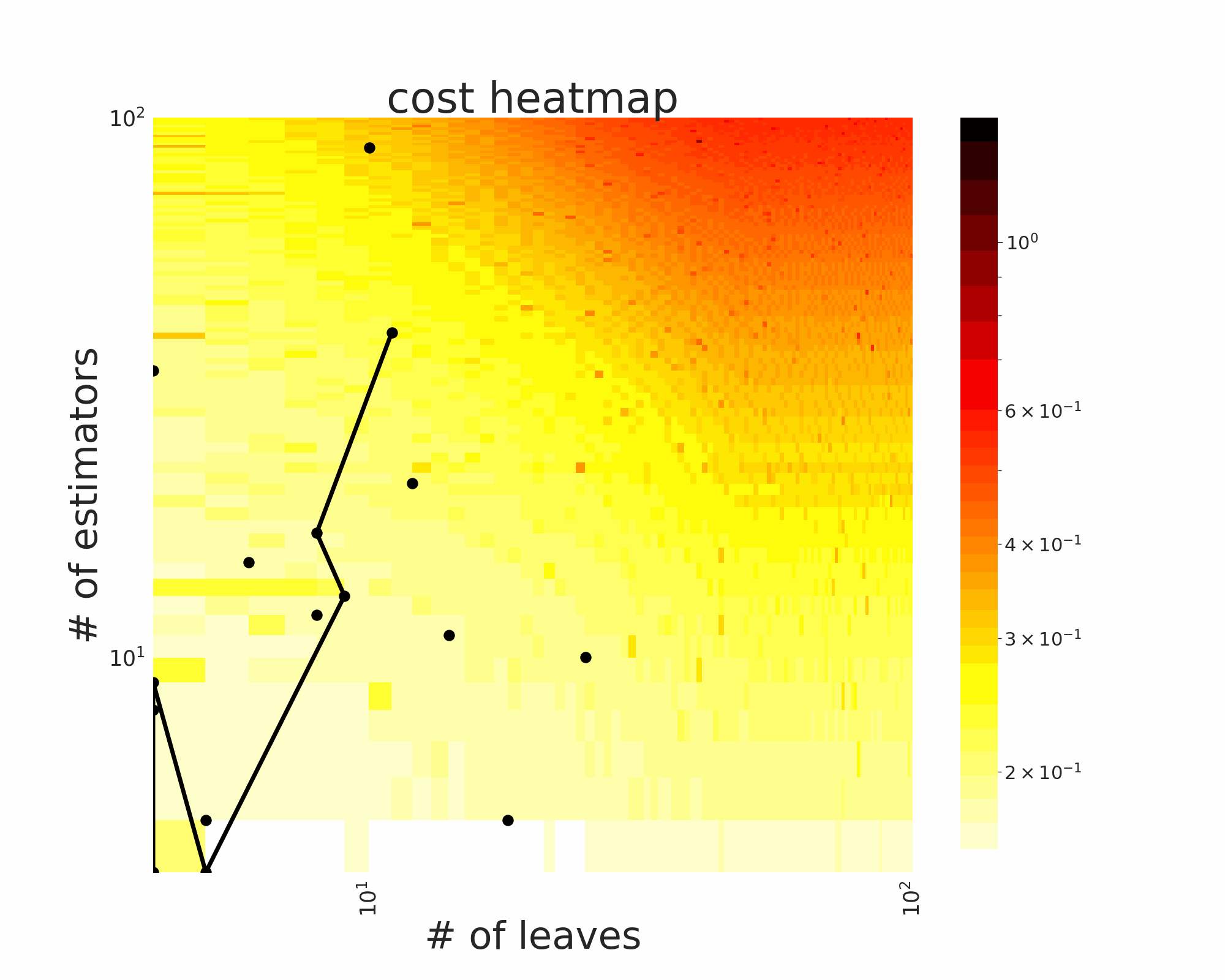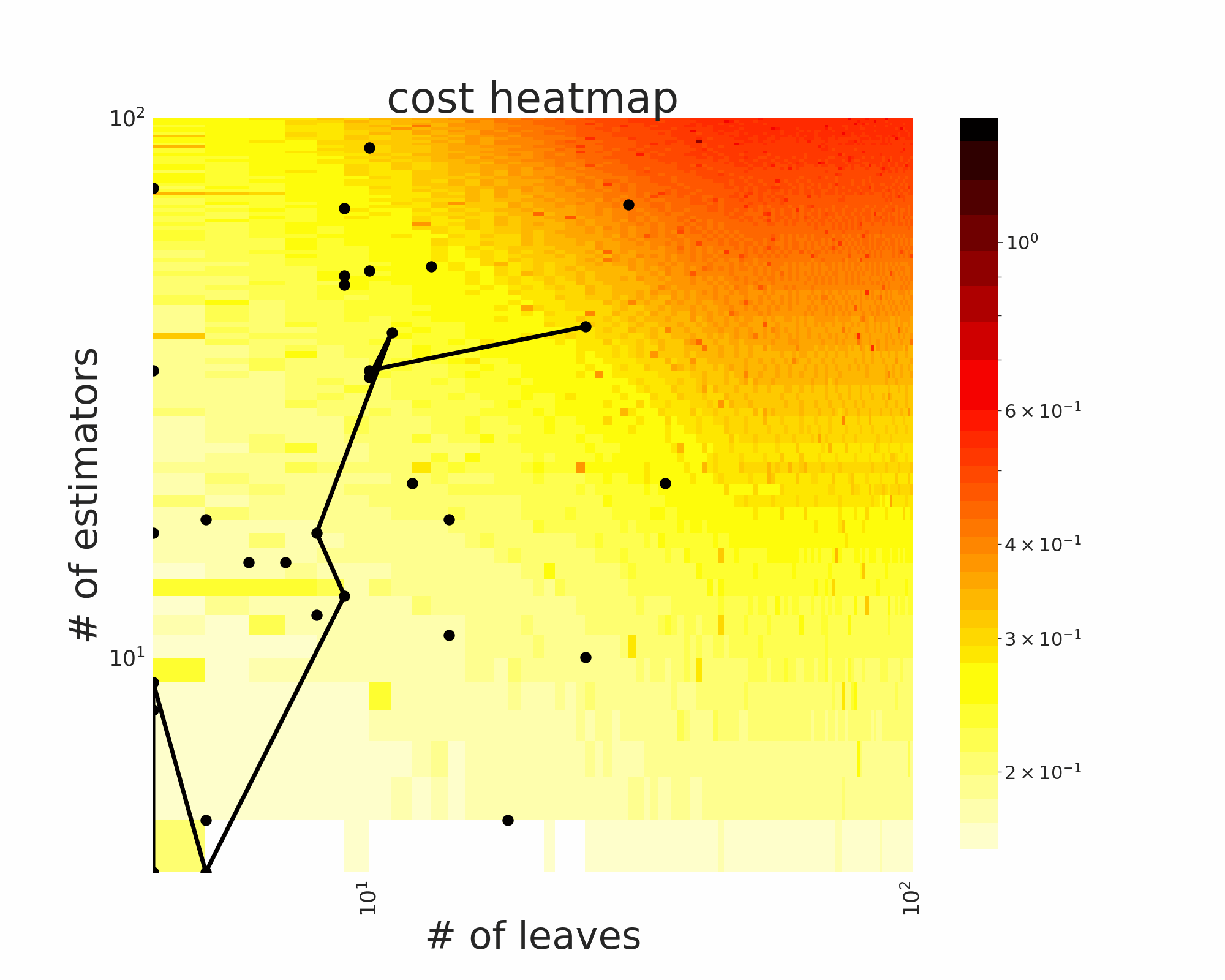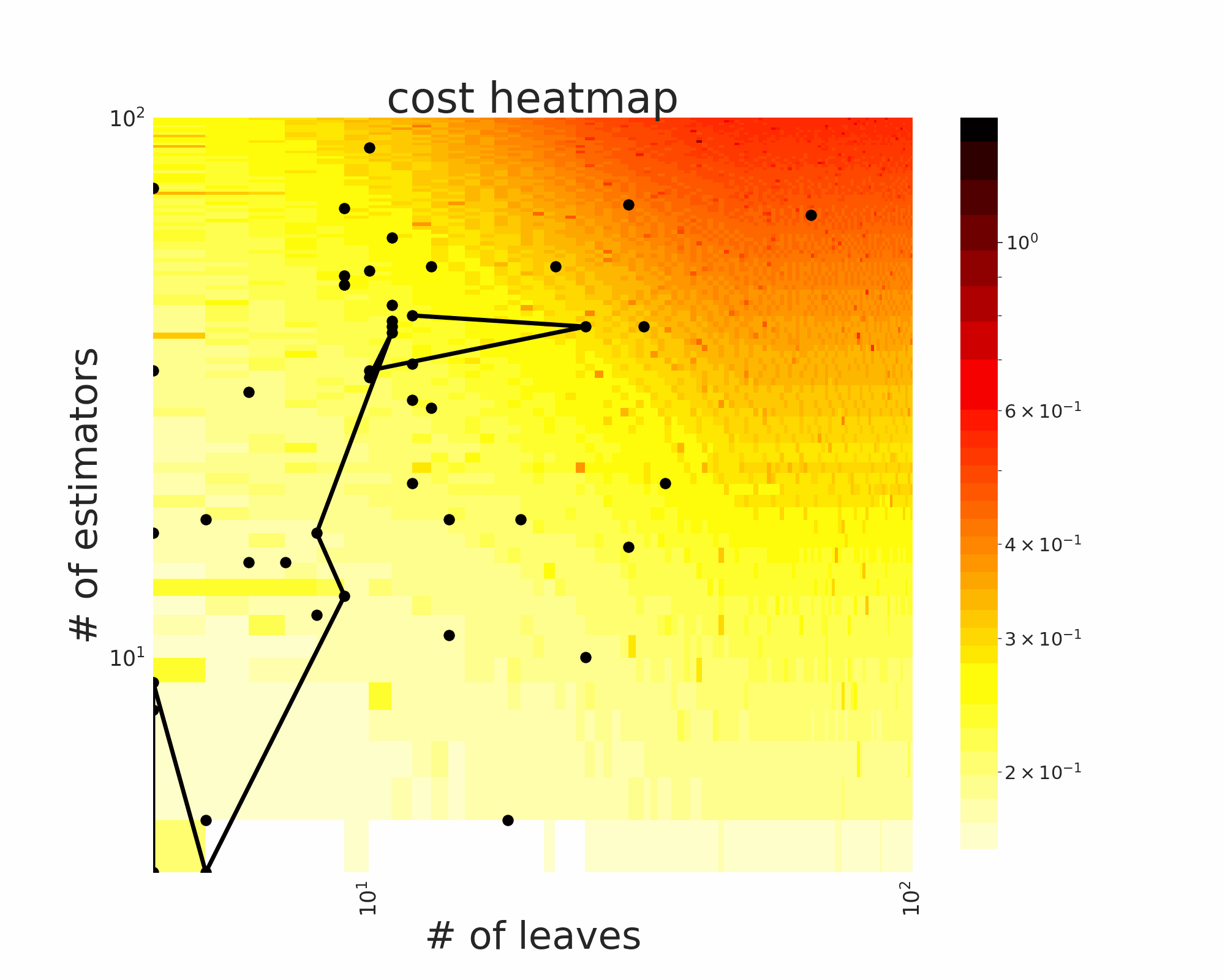From the demonstration, we can see that (1) FLOW² can quickly move toward the low-loss region, showing good convergence property and (2) FLOW² tends to avoid exploring the high-cost region until necessary.

Example:

from flaml import CFO
tune.run(...
    search_alg=CFO(low_cost_partial_config=low_cost_partial_config),
)

Recommended scenario: There exist cost-related hyperparameters and a low-cost initial point is known before optimization. If the search space is complex and CFO gets trapped into local optima, consider using BlendSearch.

BlendSearch: Economical Hyperparameter Optimization With Blended Search Strategy

BlendSearch combines local search with global search. It leverages the frugality of CFO and the space exploration ability of global search methods such as Bayesian optimization. Like CFO, BlendSearch requires a low-cost initial point as input if such point exists, and starts the search from there. Different from CFO, BlendSearch will not wait for the local search to fully converge before trying new start points. The new start points are suggested by the global search method and filtered based on their distance to the existing points in the cost-related dimensions. BlendSearch still gradually increases the trial cost. It prioritizes among the global search thread and multiple local search threads based on optimism in face of uncertainty.

Example:

# require: pip install flaml[blendsearch]
from flaml import BlendSearch
tune.run(...
    search_alg=BlendSearch(low_cost_partial_config=low_cost_partial_config),
)

Recommended scenario: Cost-related hyperparameters exist, a low-cost initial point is known, and the search space is complex such that local search is prone to be stuck at local optima.

Suggestion about using larger search space in BlendSearch. In hyperparameter optimization, a larger search space is desirable because it is more likely to include the optimal configuration (or one of the optimal configurations) in hindsight. However the performance (especially anytime performance) of most existing HPO methods is undesirable if the cost of the configurations in the search space has a large variation. Thus hand-crafted small search spaces (with relatively homogeneous cost) are often used in practice for these methods, which is subject to idiosyncrasy. BlendSearch combines the benefits of local search and global search, which enables a smart (economical) way of deciding where to explore in the search space even though it is larger than necessary. This allows users to specify a larger search space in BlendSearch, which is often easier and a better practice than narrowing down the search space by hand.

For more technical details, please check our papers.

Frugal Optimization for Cost-related Hyperparameters. Qingyun Wu, Chi Wang, Silu Huang. AAAI 2021.

@inproceedings{wu2021cfo,
    title={Frugal Optimization for Cost-related Hyperparameters},
    author={Qingyun Wu and Chi Wang and Silu Huang},
    year={2021},
    booktitle={AAAI'21},
}

Economical Hyperparameter Optimization With Blended Search Strategy. Chi Wang, Qingyun Wu, Silu Huang, Amin Saied. ICLR 2021.

@inproceedings{wang2021blendsearch,
    title={Economical Hyperparameter Optimization With Blended Search Strategy},
    author={Chi Wang and Qingyun Wu and Silu Huang and Amin Saied},
    year={2021},
    booktitle={ICLR'21},
}

Targeted Hyperparameter Optimization with Lexicographic Preferences Over Multiple Objectives. Shaokun Zhang, Feiran Jia, Chi Wang, Qingyun Wu. ICLR 2023 (notable-top-5%).

@inproceedings{zhang2023targeted,
    title={Targeted Hyperparameter Optimization with Lexicographic Preferences Over Multiple Objectives},
    author={Shaokun Zhang and Feiran Jia and Chi Wang and Qingyun Wu},
    booktitle={International Conference on Learning Representations},
    year={2023},
    url={https://openreview.net/forum?id=0Ij9_q567Ma}
}

Basic Tuning Procedure​

Tuning objective​

Search space​

Details and guidelines on hyperparameter search space​

Cost-related hyperparameters​

Tuning constraints​

Put together​

Result analysis​

Advanced Tuning Options​

More constraints on the tuning​

config_constraints vs metric_constraints:​

Parallel tuning​

Trial scheduling​

1. An authentic scheduler implemented in FLAML (scheduler='flaml').​

2. A scheduler of the TrialScheduler class from ray.tune.​

Warm start​

Reproducibility​

Lexicographic Objectives​

Hyperparameter Optimization Algorithm​

CFO: Frugal Optimization for Cost-related Hyperparameters​

BlendSearch: Economical Hyperparameter Optimization With Blended Search Strategy​

Basic Tuning Procedure

Tuning objective

Search space

Details and guidelines on hyperparameter search space

Cost-related hyperparameters

Tuning constraints

Put together

Result analysis

Advanced Tuning Options

More constraints on the tuning

`config_constraints` vs `metric_constraints`:

Parallel tuning

Trial scheduling

1. An authentic scheduler implemented in FLAML (`scheduler='flaml'`).

2. A scheduler of the `TrialScheduler` class from `ray.tune`.

Warm start

Reproducibility

Lexicographic Objectives

Hyperparameter Optimization Algorithm

CFO: Frugal Optimization for Cost-related Hyperparameters

BlendSearch: Economical Hyperparameter Optimization With Blended Search Strategy