Python Data Balance Analysis

Context

Data Balance Analysis is relevant for the overall understanding of datasets, but is essential to building Machine Learning models in a responsible way, especially in term of fairness. It is all too easy to build an ML Model that produces biased results for subsets of the population by training or testing the model on biased ground truth data. There are multiple case studies of biased models assisting in granting loans healthcare, recruitment opportunities and many other decision-making tasks. In most of these examples, the data on which these models are trained was the common issue. These findings emphasize how important it is for model creators and auditors to analyze data balance:

• to measure training data across various sub-populations

• to ensure the data has good coverage, and a balanced representation of labels across sensitive categories and category combinations

• and to check that the test data is representative of the target population

In summary, Data Balance Analysis has the following benefits when used for building ML models.

• Reduces the risk of unbalanced models by:

  • ensuring service fairness and reducing the costs of ML building by identifying data representation gaps early on

  • prompting data scientists to seek mitigation steps before proceeding on the training portion of Machine Learning model development

• Enables easy end-to-end debugging of ML systems in combination with Fairlearn by providing a clear view if an issue in a model is tied to the data or the model itself.

Usage

Data Balance Analysis supports three different types of metrics.

• FeatureMeasures - supervised (requires a label column)

• DistributionMeasures - unsupervised (does not require a label column)

• AggregateMeasures - unsupervised (does not require a label column)

Example Notebook

[Adult Census Income Dataset] ()

1. First we import all of the classes we are interested in.

import sys
sys.path.append('../../notebooks')

from raimitigations.databalanceanalysis import (
    FeatureBalanceMeasure,
    DistributionBalanceMeasure,
    AggregateBalanceMeasure,
)
import pandas as pd

from download import download_datasets

2. Load the dataset, define the features of interest and ensure that the label column is binary. Currently, the FeatureBalance measure calculator only supports binary labels.

For example:

data_dir = "../../datasets/"
download_datasets(data_dir)

df = pd.read_csv(data_dir + "AdultCensusIncome.csv", skipinitialspace=True)

sensitive_features = ["Gender", "Race"]
label_col = "income"

# convert to 0 and 1 encoding
df[label_col] = df[label_col].apply(lambda x: 0 if x == "<=50K" else 1)

3. Create an instance of the FeatureMeasure class and set the sensitives to the column you are interested in seeing and the label column to the name of the column of interest.

For example:

cols_of_interest = ["race", "sex"]
label_col = "income"
feature_measures = FeatureBalanceMeasure(cols_of_interest, label_col)
feature_measures.measures(df)

	ClassA	ClassB	FeatureName	dp	pmi	sdc	ji	krc	llr	t_test	ttest_pvalue
0	White	Black	race	0.131980	0.725320	0.164302	0.212784	-5.412507	2.911817	-1.354903	0.123458
1	White	Asian-Pac-Islander	race	-0.009780	-0.037512	0.168515	0.217291	-8.742759	3.249841	-2.582092	0.030596
2	White	Amer-Indian-Eskimo	race	0.140104	0.793149	0.195180	0.244934	-14.433135	5.286723	-4.895847	0.004034
3	White	Other	race	0.163609	1.020118	0.196514	0.246278	-15.322864	5.651366	-5.256855	0.003134
4	Black	Asian-Pac-Islander	race	-0.141760	-0.762832	0.004213	0.004507	-3.330252	0.338024	-1.227189	0.143519
5	Black	Amer-Indian-Eskimo	race	0.008124	0.067829	0.030878	0.032150	-9.020628	2.374906	-3.540944	0.011997
6	Black	Other	race	0.031629	0.294798	0.032212	0.033494	-9.910357	2.739549	-3.901952	0.008756
7	Asian-Pac-Islander	Amer-Indian-Eskimo	race	0.149884	0.830661	0.026665	0.027642	-5.690376	2.036882	-2.313755	0.040847
8	Asian-Pac-Islander	Other	race	0.173389	1.057630	0.027999	0.028987	-6.580105	2.401525	-2.674763	0.027765
9	Amer-Indian-Eskimo	Other	race	0.023505	0.226969	0.001334	0.001344	-0.889729	0.364643	-0.361008	0.368176
0	Male	Female	sex	0.196276	1.027159	0.161486	0.222413	-0.880102	1.731753	-0.372541	0.386486

4. Create an instance of the DistributionMeasures class and set the sensitive columns to the columns you are interested in seeing.

For example:

distribution_measures = DistributionBalanceMeasure(["race", "sex"])
distribution_measures.measures(df)

	FeatureName	kl_divergence	js_dist	wasserstein_dist	inf_norm_dist	total_variation_dist	chi_sq_p_value	chi_sq_stat
0	race	1.055793	0.510400	0.261709	0.654274	0.654274	0.0	87941.889193
1	sex	0.058407	0.121735	0.169205	0.169205	0.169205	0.0	3728.950616

5. Create an instance of the AggregateMeasures class and set the sensitive columns parameter to the columns of interest.

aggregate_measures = AggregateBalanceMeasure(["race"])
aggregate_measures.measures(df)

	theil_l_index	theil_t_index	atkinson_index
0	1.4678	1.055793	0.769568

Explanations of Data Balance Measures

Feature Balance Measures

Feature Balance Measures allow us to see whether each combination of sensitive feature is receiving the positive outcome (true prediction) at balanced probability.

In this context, we define a feature balance measure, also referred to as the parity, for label y as the difference between the association metrics of two different sensitive classes \(([x_A, x_B])\), with respect to the association metric \((A(x_i, y))\). That is:

\[parity(y \vert x_A, x_B, A(\cdot)) \coloneqq A(x_A, y) - A(x_B, y)\]

Using the dataset, we can see if the various sexes and races are receiving >50k income at equal or unequal rates.

Note: Many of these metrics were influenced by this paper Measuring Model Biases in the Absence of Ground Truth.

Association Metric	Family	Description	Interpretation	Reference
Demographic Parity	Fairness	Proportion of each segment of a protected class (e.g. gender) should receive the positive outcome at equal rates.	As close to 0 means better parity. \((DP = P(Y \vert A = Male) - P(Y \vert A = Female))\). Y = Positive label rate.	Link
Pointwise Mutual Information (PMI), normalized PMI	Entropy	The PMI of a pair of feature values (ex: Gender=Male and Gender=Female) quantifies the discrepancy between the probability of their coincidence given their joint distribution and their individual distributions (assuming independence).	Range (normalized) [-1, 1]. -1 for no co-occurences. 0 for co-occurences at random. 1 for complete co-occurences.	Link
Sorensen-Dice Coefficient (SDC)	Intersection-over-Union	Union Used to gauge the similarity of two samples. Related to F1 score.	Equals twice the number of elements common to both sets divided by the sum of the number of elements in each set.	Link
Jaccard Index	Intersection-over-Union	Similar to SDC, guages the similarity and diversity of sample sets.	Equals the size of the intersection divided by the size of the union of the sample sets.	Link
Kendall Rank Correlation	Correlation and Statistical Tests	Used to measure the ordinal association between two measured quantities.	High when observations have a similar rank and low when observations have a dissimilar rank between the two variables.	Link
Log-Likelihood Ratio	Correlation and Statistical Tests	Statistical Tests Calculates the degree to which data supports one variable versus another. Log of the likelihood ratio, which gives the probability of correctly predicting the label in ratio to probability of incorrectly predicting label.	If likelihoods are similar, it should be close to 0.	Link
t-test	Correlation and Statistical Tests	Used to compare the means of two groups (pairwise).	Value looked up in t-Distribution tell if statistically significant or not.	Link

Distribution Balance Measures

Distribution Balance Measures allow us to compare our data with a reference distribution (currently only uniform distribution is supported as a reference distribution). They are calculated per sensitive column and do not depend on the label column.

For example, let’s assume we have a dataset with 9 rows and a Gender column, and we observe that:

• “Male” appears 4 times

• “Female” appears 3 times

• “Other” appears 2 times

Assuming the uniform distribution:

\[ReferenceCount \coloneqq \frac{numRows}{numFeatureValues}\]

\[ReferenceProbability \coloneqq \frac{1}{numFeatureValues}\]

Feature Value	Observed Count	Reference Count	Observed Probability	Reference Probabiliy
Male	4	9/3 = 3	4/9 = 0.44	3/9 = 0.33
Female	3	9/3 = 3	3/9 = 0.33	3/9 = 0.33
Other	2	9/3 = 3	2/9 = 0.22	3/9 = 0.33

We can use distance measures to find out how far our observed and reference distributions of these feature values are. Some of these distance measures include:

Measure	Description	Interpretation	Reference
KL Divergence	Measure of how one probability distribution is different from a second, reference probability distribution. Measure of the information gained when one revises one’s beliefs from the prior probability distribution Q to the posterior probability distribution P. In other words, it is the amount of information lost when Q is used to approximate P.	Non-negative. 0 means P = Q.	Link
Jenson-Shannon Distance	Measuring the similarity between two probability distributions. Symmetrized and smoothed version of the Kullback–Leibler (KL) divergence. Square root of Jenson-Shannon Divergence.	Range [0, 1]. 0 means perfectly same to balanced distribution.	Link
Wasserstein Distance	This distance is also known as the earth mover’s distance, since it can be seen as the minimum amount of “work” required to transform u into v, where “work” is measured as the amount of distribution weight that must be moved, multiplied by the distance it has to be moved.	Non-negative. 0 means P = Q.	Link
Infinity Norm Distance	Distance between two vectors is the greatest of their differences along any coordinate dimension. Also called Chebyshev distance or chessboard distance.	Non-negative. 0 means same distribution.	Link
Total Variation Distance	It is equal to half the L1 (Manhattan) distance between the two distributions. Take the difference between the two proportions in each category, add up the absolute values of all the differences, and then divide the sum by 2.	Non-negative. 0 means same distribution.	Link
Chi-Squared Test	The chi-square test tests the null hypothesis that the categorical data has the given frequencies given expected frequencies in each category.	p-value gives evidence against null-hypothesis that difference in observed and expected frequencies is by random chance.	Link

Aggregate Balance Measures

Aggregate Balance Measures allow us to obtain a higher notion of inequality. They are calculated on the set of all sensitive columns and do not depend on the label column.

These measures look at distribution of records across all combinations of sensitive columns. For example, if Sex and Race are specified as sensitive features, it then tries to quantify imbalance across all combinations of the two specified features - (Male, Black), (Female, White), (Male, Asian-Pac-Islander), etc.

Measure	Description	Interpretation	Reference
Atkinson Index	It presents the percentage of total income that a given society would have to forego in order to have more equal shares of income between its citizens. This measure depends on the degree of society aversion to inequality (a theoretical parameter decided by the researcher), where a higher value entails greater social utility or willingness by individuals to accept smaller incomes in exchange for a more equal distribution. An important feature of the Atkinson index is that it can be decomposed into within-group and between-group inequality.	Range [0, 1]. 0 if perfect equality. 1 means maximum inequality. In our case, it is the proportion of records for a sensitive columns’ combination.	Link
Theil T Index	GE(1) = Theil’s T and is more sensitive to differences at the top of the distribution. The Theil index is a statistic used to measure economic inequality. The Theil index measures an entropic “distance” the population is away from the “ideal” egalitarian state of everyone having the same income.	If everyone has the same income, then T_T equals 0. If one person has all the income, then T_T gives the result (ln N). 0 means equal income and larger values mean higher level of disproportion.	Link
Theil L Index	GE(0) = Theil’s L and is more sensitive to differences at the lower end of the distribution. Logarithm of (mean income)/(income i), over all the incomes included in the summation. It is also referred to as the mean log deviation measure. Because a transfer from a larger income to a smaller one will change the smaller income’s ratio more than it changes the larger income’s ratio, the transfer-principle is satisfied by this index.	Same interpretation as Theil T Index.	Link

Mitigation

It will not be a stretch to say that every real-world dataset has caveats, biases, and imbalances. Data collection is costly. Data Imbalance mitigation or de-biasing data is an area of research. There are many techniques available at various stages of ML lifecycle i.e., during pre-processing, in-processing, and post processing. Here we outline a couple of pre-processing techniques -

Resampling

This involves under-sampling from majority class and over-sampling from minority class. Most naïve way to over-sample would be duplicate records and under-sample would be to remove records at random.

• Caveats:

  1. Under-sampling may remove valuable information.

  2. Over-sampling may cause overfitting and poor generalization on test set.

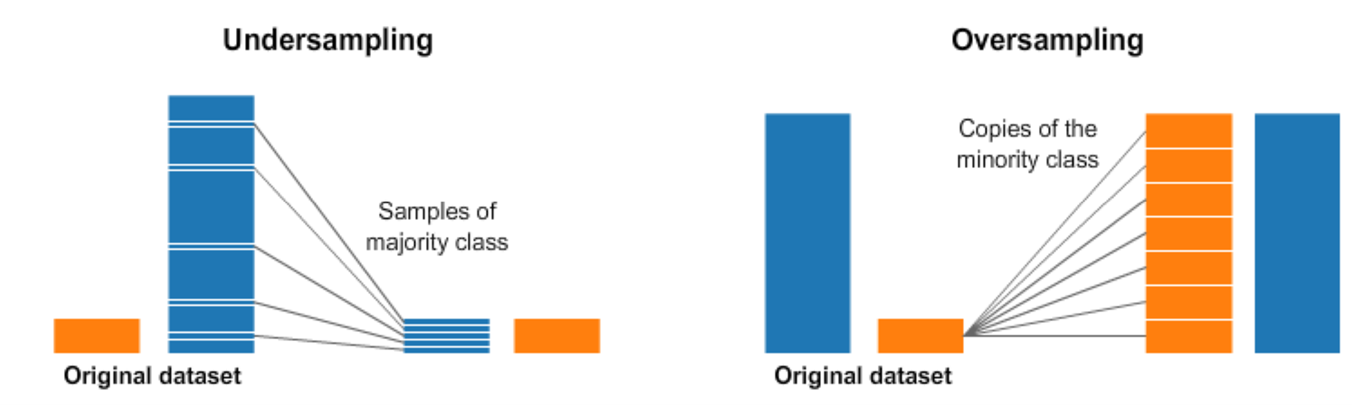
There are smarter techniques to under-sample and over-sample in literature and implemented in Python’s imbalanced-learn package.

For example, we can cluster the records of the majority class, and do the under-sampling by removing records from each cluster, thus seeking to preserve information.

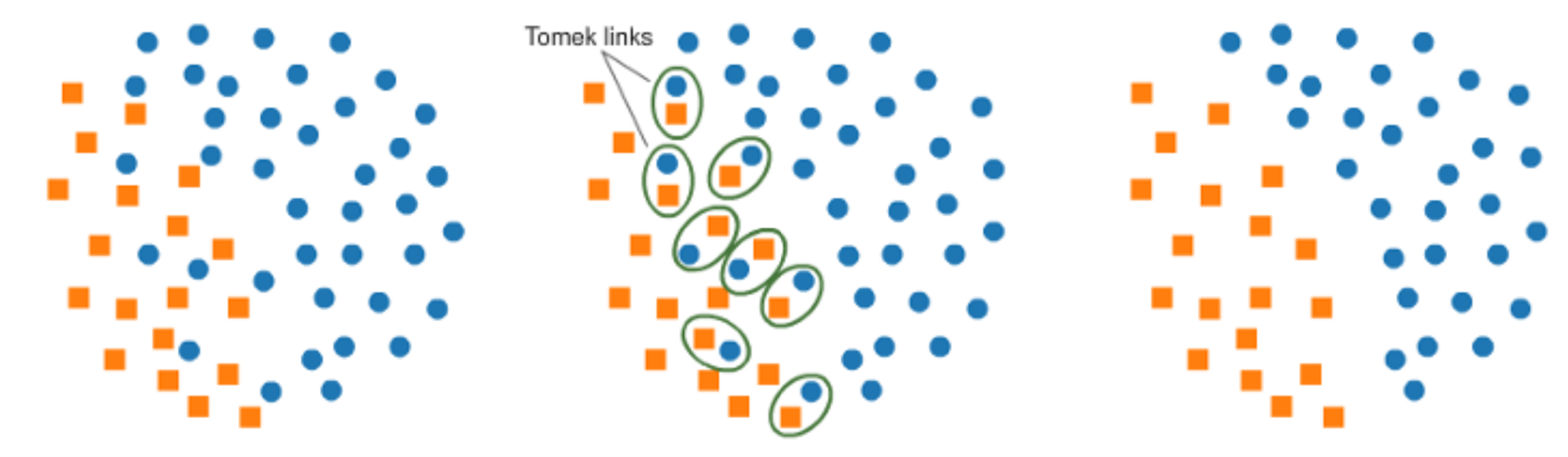
One technique of under-sampling is use of Tomek Links. Tomek links are pairs of very close instances but of opposite classes. Removing the instances of the majority class of each pair increases the space between the two classes, facilitating the classification process. A similar way to under-sample majority class is using Near-Miss. It first calculates the distance between all the points in the larger class with the points in the smaller class. When two points belonging to different classes are very close to each other in the distribution, this algorithm eliminates the datapoint of the larger class thereby trying to balance the distribution.

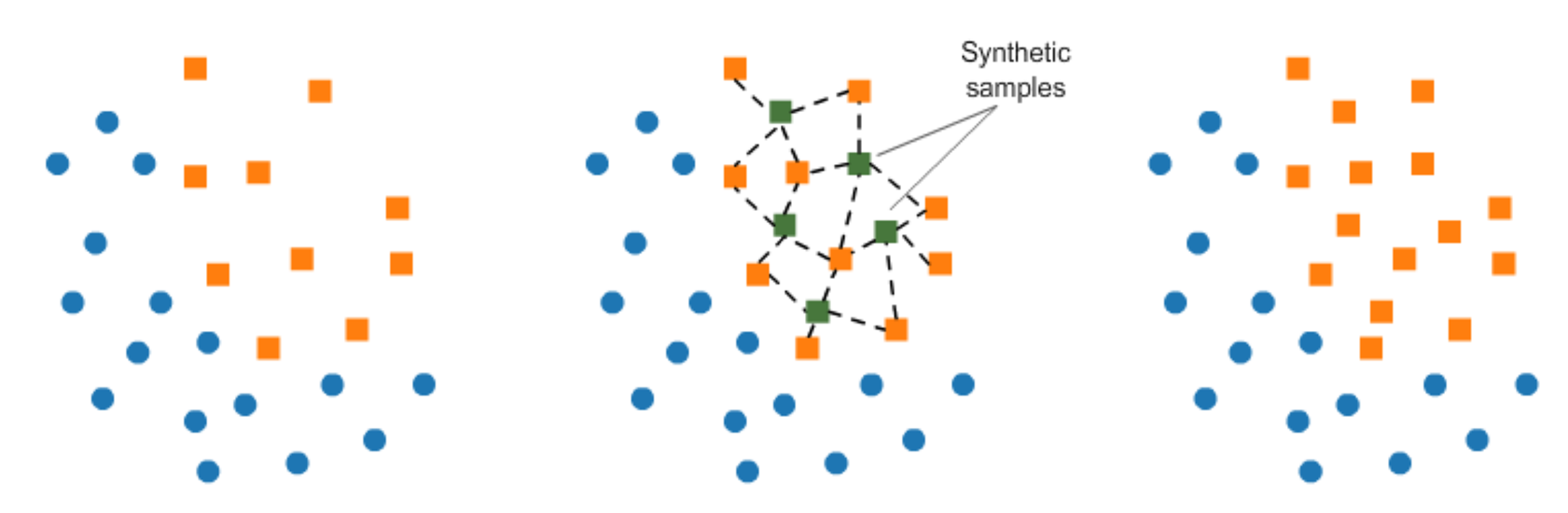
In over-sampling, instead of creating exact copies of the minority class records, we can introduce small variations into those copies, creating more diverse synthetic samples. This technique is called SMOTE (Synthetic Minority Oversampling Technique). It randomly picks a point from the minority class and computes the k-nearest neighbors for this point. The synthetic points are added between the chosen point and its neighbors.

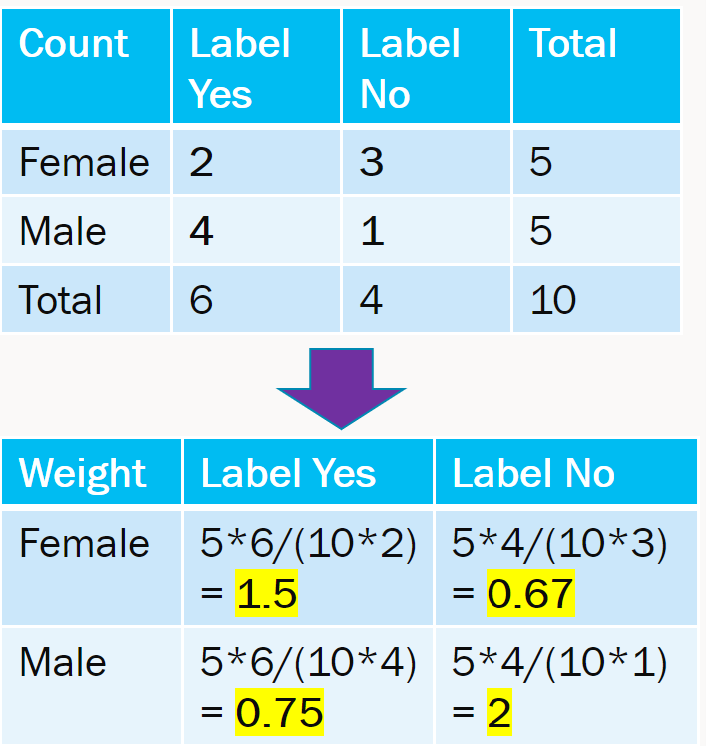
Reweighting

There is an expected and observed value in each table cell. The weight is essentially expected / observed value. This is easy to extend to multiple features with more than 2 groups. The weights are then incorporated in loss function of model training.

Source: This notebook is adaptation of this notebook in the SynapseML documentation https://microsoft.github.io/SynapseML/docs/features/responsible_ai/Data%20Balance%20Analysis/ written by Kashyap Patel