In this tutorial, we’ll learn how to make an abstract model of a simple protocol and prove a property of it using an inductive invariant. This is usually the first step in designing and implementing a protocol in Ivy.

An invariant of a system is a formula about the system’s state that is always true. Invariants are the simplest class of properties that we specify about systems. An inductive invariant is a formula or a set of formulas that has the following key properties:

• initiation: It is true in all initial states of the program.

• consecution: If it is true in a state, then after executing any exported action, the formula remains true.

Every inductive invariant is an invariant, but not every invariant is inductive. An inductive invariant is relatively easy to prove, since we only have to verify the initiation and consecution properties, a task which Ivy can usually perform automatically. Often, though, the invariant properties we really want to prove are not inductive and we therefore require some cleverness to strengthen the desired invariant to make it inductive.

As we will see, Ivy makes this step easier by providing tools to visualize the failures of inductive proofs and suggest possible refinements to the proof.

An abstract protocol model

The following Ivy program is a very abstract model of a semaphore protocol. We have a collection of clients and a collection of servers. Each server has a semaphore which can be held by at most one client at a time.

#lang ivy1.7

type client
type server

relation link(X:client, Y:server)
relation semaphore(X:server)

after init {
    semaphore(W) := true;
    link(X,Y) := false
}

action connect(x:client,y:server) = {
  require semaphore(y);
  link(x,y) := true;
  semaphore(y) := false
}

action disconnect(x:client,y:server) = {
  require link(x,y);
  link(x,y) := false;
  semaphore(y) := true
}

export connect
export disconnect

This program declares two types client and server. At this point, we don’t know anything about these types except that there is at least one value of each type. The types client and server can be though of as representing abstract identifiers of clients and servers, respectively (when we implement this protocol, we might replace these abstract identifiers by network addresses).

The state of the protocol model consists of two relations. The relation link tells us which clients are are holding the semaphores of which servers, while semaphore tells us which servers have their semaphore “up” (that is, available to be taken).

The program contains a block code after the keywords after init. This code is executed just once when the protocol starts. It initializes the state so that all the semaphore are “up” (that is, for every server W. semaphore(W) is set to true) and there are no links (that is, for every client X and server Y, link(X,Y) is set to false). These statements are simultaneous assignments that update the given relations for many values of their parameters at once. You can recognize a simultaneous assignment by the fact that the parameters of the relations are placeholders (or wildcards) represented by capital letters.

The program exports two actions to the environment: connect and disconnect. The connect actions creates a link from client x to server y, putting the server’s semaphore down. Each action has a precondition, indicated by the require keyword. To call an action, the environment is required to satisfy its precondition. Notice that connect requires that the server’s semaphore be initially up. The disconnect action removes a link and puts the semaphore up. It requires that the link be initially established. The two export declarations at the end tell us that the environment may call connect and disconnect in arbitrary sequence, though it must obey the stated requirements.

It is important to keep in mind that this Ivy program is an abstract model of a protocol, and not the protocol’s actual implementation. The abstract actions just describe the possible high-level state transitions that the protocol can make. It doesn’t tell us how these transitions actually come about. In an implementation, the abstract connect action might be achieved by the client sending a request message to the server and the server issuing a reply.

Safety and invariant conjectures

Now we will give our abstract model a property that it must satisfy. The simplest kind of property we can specify is an invariant. This is a formula that must hold true between calls by the environment to the program’s actions (though it might be untrue temporarily while the actions are executing). In the client/server example above, we might specify that no two distinct clients can be linked to a single server at the same time. We can express this property using the following invariant assertion:

invariant ~(X ~= Z & link(X,Y) & link(Z,Y))

Once again the capital letters act as wildcards. The invariant assertion implicitly holds true for all clients X and Z and all servers Y. Another way to say this is that the placeholders X, Y and Z are implicitly universally quantified.

Proving the invariant

As mentioned above, to prove an invariant, we check that it is initially true, and that every action of the program preserves it. Ivy can do this automatically. To make the check, we use this command:

$ ivy_check client_server_example.ivy

[Note: the source files for the examples in this tutorial can be found in the subdirectory doc/examples of the Ivy source tree]. Ivy attempts the check and produces this somewhat discouraging output (with uninteresting parts omitted):

...

Initialization must establish the invariant
    client_server_example.ivy: line 30: invar2 ... PASS

...

The following set of external actions must preserve the invariant:
    ext:connect
        client_server_example.ivy: line 30: invar2 ... FAIL
    ext:disconnect
        client_server_example.ivy: line 30: invar2 ... PASS

...

error: failed checks: 1

This means that our proposed invariant may be true, but it isn’t inductive. In particular the connect action doesn’t preserve the invariant. We should take heart, however, because Ivy can give us some feedback that explains what went wrong in the form of a counterexample. A counterexample in this case is an execution of the connect action that starts in a state in which the invariant is true and ends in a state in which it is false.

We can get a graphical view of the counterexample by running the check again with the option diagnose=true, like this:

$ ivy_check diagnose=true client_server_example.ivy

Ivy pops up a window that looks like this:

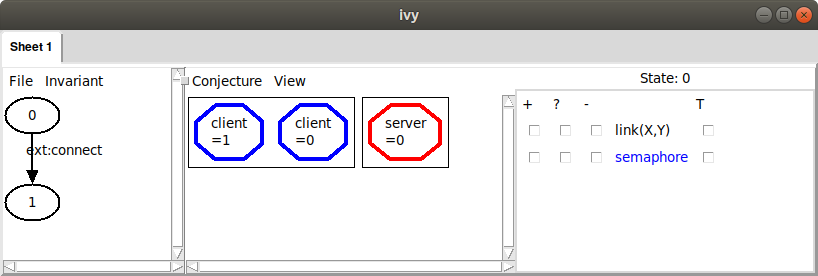
In the left pane of this window is a diagram in which each oval represents a state of the protocol and each arrow represents the execution of an action. There are two states, labeled 0 and 1. From state 0 to state 1 there is an arrow labeled with the action connect. We know something has gone wrong in the execution of connect.

In the middle pane, we see a graphical representation of state 0. Currently, all we see is that there are two clients (in other words, two values of type client) and there is one server. To learn more about the state, we can use the checkboxes on the right to enable the display of relations in this state. For example, if we check the box in the + column next to the relation link(X,Y), we’ll see an arrow from client X to server Y when the relation link(X,Y) is true. In this case, we see:

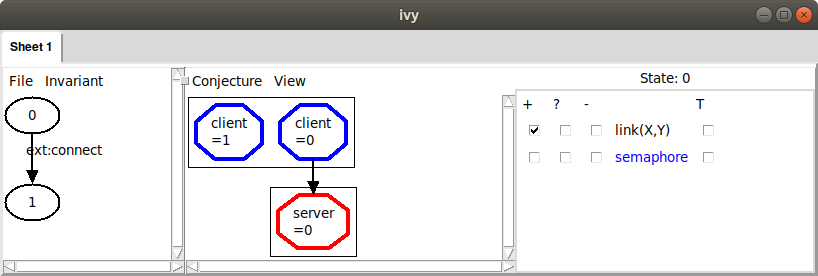
Here, we see that just one client is connected to the server, which means our invariant property is true. When we check that an invariant is inductive, the counterexample always starts in a state in which the invariant holds. If we check the box in the + column next to semaphore(X), we can begin to see a problem:

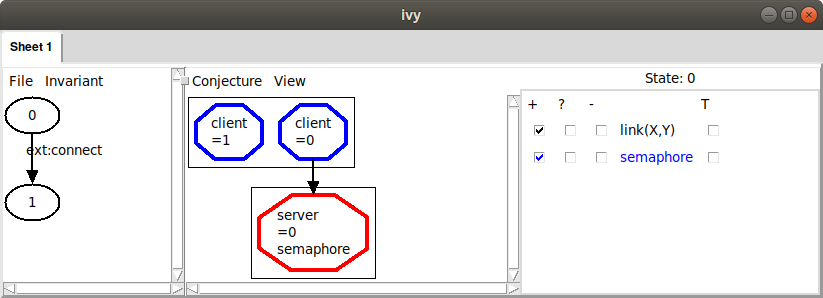
Ivy is telling us that the value of semaphore at our server is true. We had in mind, however, that the semaphore should be “down” (i.e., false) whenever a client is connected to the server. We therefore suspect that this state of the system is not possible (that is, it is not reachable from the initial state). This usually means that we need to add another formula to our invariant to rule out something bad about this state.

To see the consequence of the semaphore being up, we can move to state 1 by clicking on it. Here’s what we see:

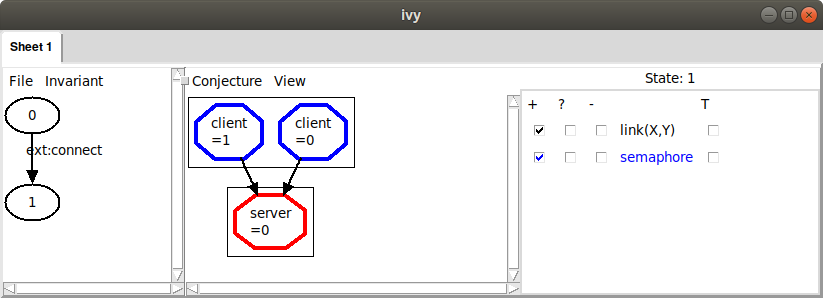
Now both clients are linked to the same server, violating our invariant property. A counterexample to induction always ends in this way. To see more detail about how we got there, we can left-click on the action connect and choose Step in. This will show us the detailed sequence of actions that got to the bad state:

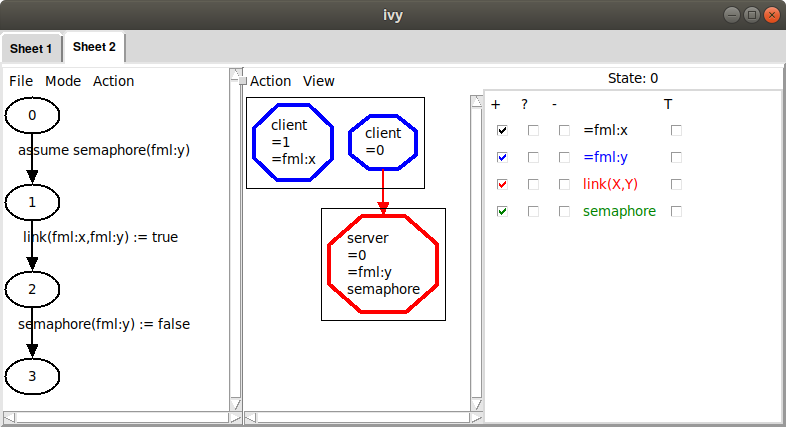
Here, we are viewing state 0 (the state that occurs just at entry to the connect action). We have checked a few boxes to display information about this state. We can see here the values of the formal parameters x and y that were provided by the environment when calling connect. In particular, the environment chose the value 1 for x, meaning that client 1 should be connected to server 0 (the only server in this case). The counterexample steps through three additional states, first testing the precondition of connect (which is true, since the semaphore is up), then establishing a link from x to y, then putting the semaphore down.

If we left-click on any statement choose Show source, the corresponding source line is displayed. As we step into action calls, we build up a sequence of tabs, corresponding to something like a stack trace of the program’s execution. Tabs can be removed by choosing Remove tab from the File menu.

At this point we understand the reason that the invariant is not inductive. The failure was caused by the fact that a client X was connected to a server Y and the semaphore at this server was up. This bad pattern caused the failure, and we conjecture that it can never actually occur. For this reason, we will strengthen our invariant with a condition that rules out the bad pattern. It is very important to understand that we do not want to rule out everything about the counterexample that is unrealistic – only those aspects that actually cause the failure.

To rule out the bad pattern, we add this new conjectured invariant to our Ivy program:

private {
    invariant ~(link(X,Y) & semaphore(Y))
}

This says that there is no client X and server Y such that X is linked to Y and the semaphore at Y is up. Notice again that the capital letters X and Y are universally quantified placeholders. We put the new invariant property in a private section just to indicate that this invariant is not of interest to users of the protocol model. It is only introduced as part of the proof of the original invariant. Now when we check the program, we get this:

...

Initialization must establish the invariant
    client_server_example.ivy: line 26: invar2 ... PASS
    client_server_example.ivy: line 34: invar3 ... PASS

Any assertions in initializers must be checked ... PASS

The following set of external actions must preserve the invariant:
    ext:connect
        client_server_example.ivy: line 26: invar2 ... PASS
        client_server_example.ivy: line 34: invar3 ... PASS
    ext:disconnect
        client_server_example.ivy: line 26: invar2 ... PASS
        client_server_example.ivy: line 34: invar3 ... PASS

...
OK

The OK at the end tells us that our invariants taken together are now inductive. This means we can be confident that the invariants always hold.

Another way to create a conjectured invariant from a bad pattern is to have Ivy gather the displayed facts and generalize them. Once we have the bad pattern displayed, as above, we use the ‘Gather’ command in the Conjecture menu. This gives us the following:

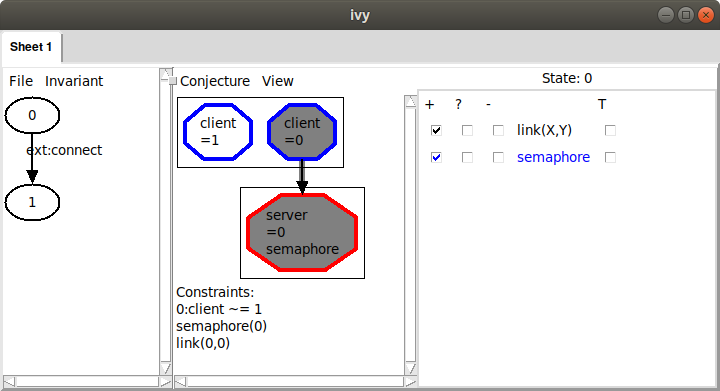
Ivy has collected three facts about the displayed state, shown under the heading ‘Constraints’. These facts are a logical representation of the bad pattern we observed graphically: there are two distinct nodes, one of which is connected to the server and the server’s semaphore is up.

Also notice that some nodes and the arcs in the graph have been highlighted to indicate that they are used in the listed facts. We can click on facts in this list to toggle them off and on. This allows us to adjust the bad pattern.

Since we think that the displayed facts form a bad pattern, we can generalize them to produce a new conjectured invariant about the program state. Choosing the Strengthen option from the Conjecture menu, we see:

Ivy is suggesting to add this fact to the list of conjectured invariants:

~(C:client ~= D & link(C,S) & semaphore(S))

Ivy has simply replaced the fixed client and sever identifiers in the gathered facts with universally quantified placeholders C, D and S. This formula says that we cannot have two distinct clients, where one of them is linked to the server and the semaphore is up. We click OK, adding this formula to our list of conjectured invariants.

We can now try checking inductiveness again with our new conjecture. We do this with the Check induction command in the Invariant menu. We see the following:

If the induction check had failed, we would see a new counterexample to induction that we would have to rule out. However, since it was successful, we now have a proof that our desired invariant holds. Of course, we want to save our new inductive invariant so that we can use it again later. We select Save invariant from the File menu and enter a file name:

Here is the content of the file:

# new conjectures

invariant ~(C:client ~= D & link(C,S) & semaphore(S))

This new invariant can be pasted into our program. Notice it is slightly different from the invariant we selected previously. That is, the bad pattern includes a second client D that is needed to violate the desired property of mutual exclusion. It turns out this doesn’t matter. This weaker invariant is still strong enough to prove the property.

Let’s consider the process we just used to arrive at an inductive invariant. We took the following steps:

• Find a simple counterexample to induction

• Identify relevant facts about the counter-example (the bad pattern)

• Generalize to form a universally quantified invariant conjecture

The first and last steps were done automatically by Ivy. However, we performed the second step manually, by select which relations to display.

This process is something of an art and can be confusing. For example, it sometimes happens that a condition we thought was a bad pattern is actually reachable. In this case, we have to backtrack and perhaps rule out a more specific pattern. Fortunately, Ivy provides some tools to help us make these choices.

Generalization tools

Ivy has some techniques built in to help us identify bad patterns. Let’s to back to the counterexample we found to inductiveness of our proposed invariant:

We can ask Ivy to try to generalize from the counterexample, by finding a bad pattern in state 0 that is sufficient to cause our proposed invariant to fail at state 1. To do this we choose Diagram from the Invariant menu. This produces the following display:

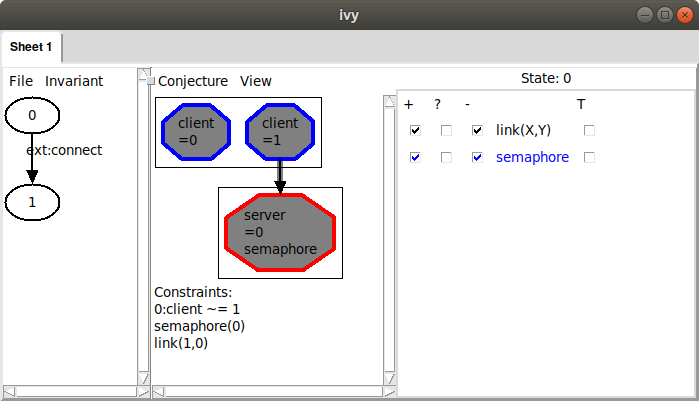
Ivy has drawn a diagram of a possible bad pattern it has identified in the state. The pattern includes the two clients and the server from our counterexample, which are highlighted in the diagram. In addition, it includes the link from client 1 to the server, and the fact that the semaphore is true at the server. These facts are listed below the diagram under the heading ‘Constraints’. Ivy has determined that these conditions are sufficient to cause the invariant to fail.

Since we agree that this is a bad pattern, we can use the Strengthen option from the Conjecture menu, as above, to produce a conjectured invariant that rules it out. In this simple case, the strengthening of the invariant has been done fully automatically.

However, as we noted above, this bad pattern contains in irrelevant fact, and we might want to drop it to get a stronger conjecture that rules out more cases. That is, our bad pattern requires that there are two distinct nodes, 0 and 1. In fact, we do need two nodes to have a safety violation (that is, to have two nodes connected to one server). Notice, though, that if we drop this fact from the pattern, we still have a pattern that we can rule out, that is, semaphore(0) and link(0,0).

To check this idea, we remove the irrelevant fact from the pattern by clicking on it. The unwanted fact becomes gray:

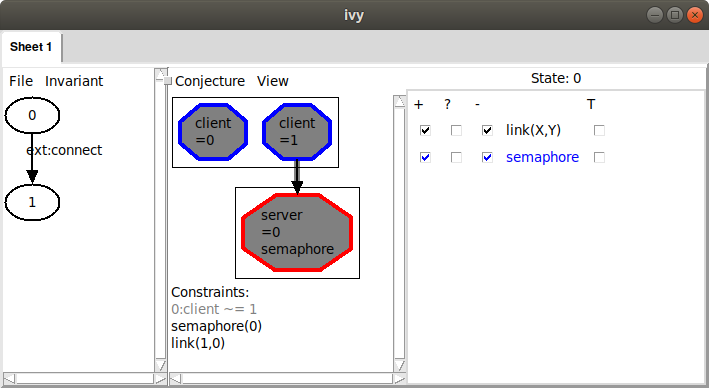
When we strengthen using this pattern, we get this:

That is, our new conjecture says that no client can be connected to a server with the semaphore up, but it doesn’t depend on the existence of any other client. We can verify that with this conjecture, we still have an inductive invariant.

This illustrates an important point about inductive invariants: there are many of them. This give us the flexibility to find a simple one. By dropping a fact from the bad pattern, we effectively generalized it. That is, we ruled out a larger class of states, so in effect we made a stronger conjecture.

Ivy can often discover automatically that a bad pattern can be simplified. One way to do this is to use bounded reachability. After Gather, Instead of manually eliminating the unwanted facts, we can select Minimize from the Conjecture menu. Ivy ask for the number of steps to check. Somewhat arbitrarily, we choose four. This is the result we get:

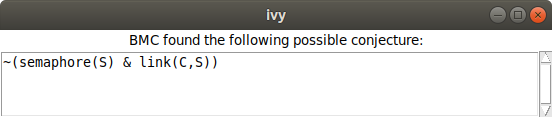
Ivy has recognized that there is a more general pattern that can be ruled out if we consider only four steps of execution of the protocol. Its conjecture is that if any client is connected to a server, that server’s semaphore is down. This fact is definitely true after four steps of execution, but it’s still a conjecture. If we’re suspicious that it might not be invariantly true, we could try five steps, six steps, and so on until we are convinced, or until the Ivy gets too slow.

We can add Ivy’s generalized conjecture to our set using Strengthen, which completes the proof.

Things that go wrong

At some point, we will make a conjecture that is just plain wrong, in the sense that it is not always true. Before clicking Strengthen, it’s a good idea to try Bounded check to see if the proposed bad pattern can actually occur within some fixed number of steps.

To see how this goes, suppose we get into this situation:

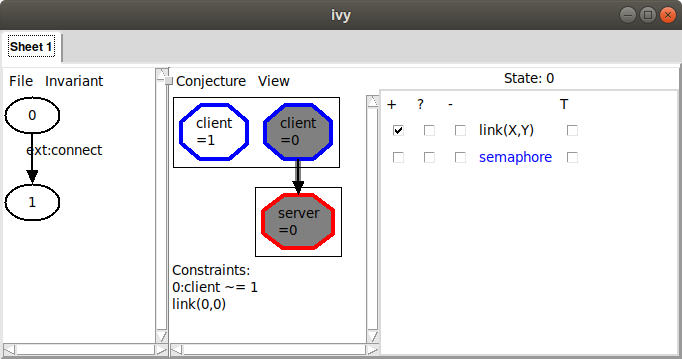
Here, we didn’t consider the semaphore and we conjectured a bad pattern in which there is a client connected to a server. Obviously (or hopefully) this is actually reachable. To see why this is a bad conjecture, we can select Bounded check from the Conjecture menu. Here’s what we see when we choose one step:

Ivy tried the conjecture that node client is connected to any server for one step and found it false. If we click View, here is what we see:

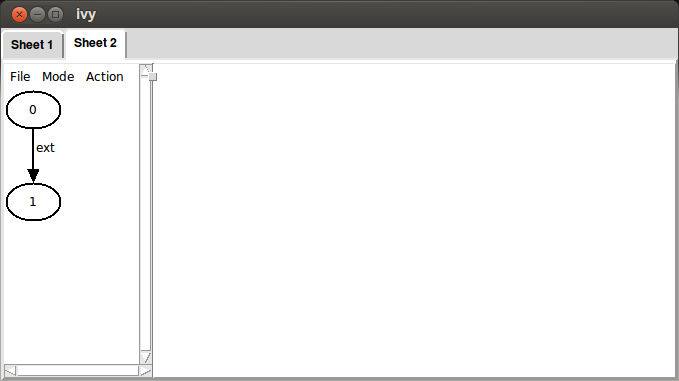
Ivy has created a new tab in the interface with a trace consisting of two steps. The arrow represents a transition from state 0 to state 1 using the ext action. This represents an action of the environment. Clicking on state 0, and checking the link and semaphore relations, we see the following:

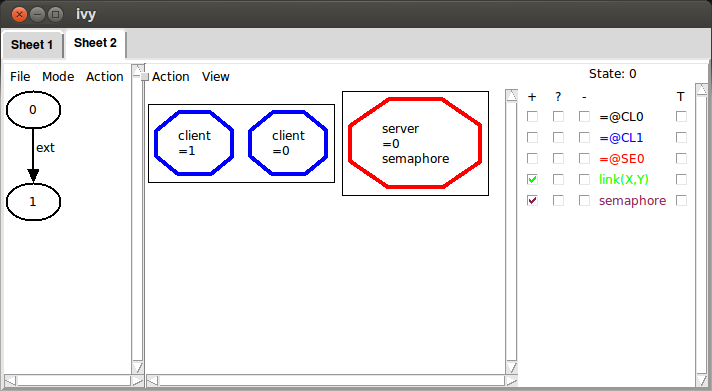
That is, in the initial state there are two clients and one server, the semaphore of the server is up and there are no links.

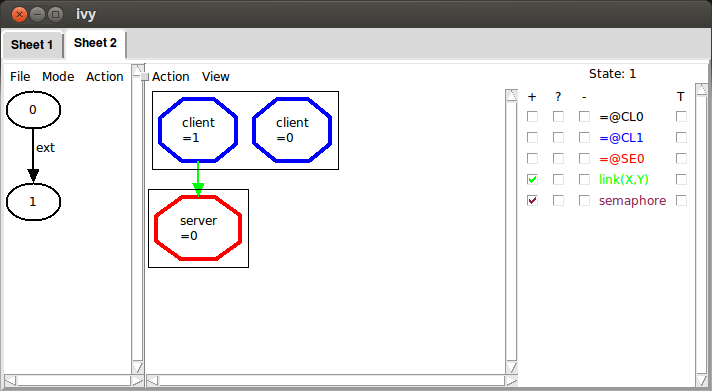
Now, clicking on state 1, we see our proposed bad pattern. This means that the pattern can actually occur.

Removing a failed conjecture

Even with bounded checking, it is still possible that we could mistakenly strengthen the invariant with a conjecture that isn’t true. If this happens, or if we regret a conjecture for any other reason, we can remove it using the Weaken operation in the Invariant menu:

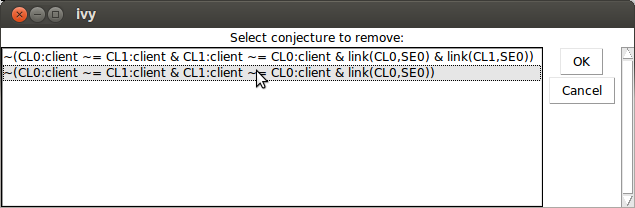
This dialog can be resized to see long formulas.

Summary

We prove invariant properties by induction. If our proposed invariant is not inductive, Ivy generates a counterexample to induction or CTI. Ivy tries to generate the simplest possible counterexample.

A CTI can be eliminated by strengthening the proposed inductive invariant. To do this, we identify a bad pattern in the CTI. This is done in the following steps:

• Use the check boxes to display relevant information
• Gather the displayed facts
• Select relevant facts by clicking to enable or disable them.
• Strengthen the invariant by generalizing the bad pattern.

You can get some help from Ivy in this process:

• Use Diagram to have Ivy try to guess a bad pattern.
• Use Bounded check to see if the bad pattern is reachable in a given number of steps.
• Use Minimize to generalize the pattern by dropping un-needed facts.

To debug a counterexample, left-click on an action call and choose Step in. The View source operation can be used to find the action in the source file.

When you are convinced that a bad pattern should be ruled out, use Strengthen to generalize it to a universal conjecture and add it to the proposed invariant. To remove a conjecture from the proposed invariant, use Weaken.

When Check induction produces no CTI, the conjectured invariant is in fact a safety invariant. You can save it for future use with the Save invariant operation.