Erdos-Renyi (ER) Model¶
[1]:
import graspologic
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
Erdos-Renyi (ER) graphs are the simplest generative model. We assume that each edge for all pairs of vertices is sampled independently from all the edges. There are two ways to parameterize the model:
ER(n, p) - this model specifies the number of vertices, \(n\), and each pair of vertices has \(p\) probability of an edge existing between the two.
ER(n, m) - this model specifies the number of vertices, \(n\), and the total number of edges \(m\).
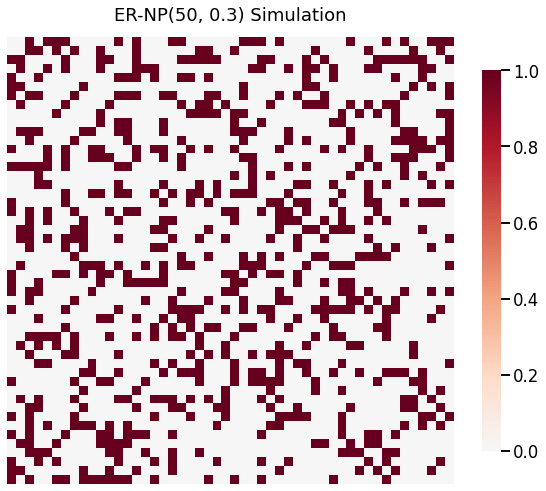
Below, we sample two binary graphs (undirected and no self-loops) \(G_1 \sim ER_{NP}(50, 0.3)\) and \(G_2 \sim ER_{NM}(50, 250)\).
[2]:
from graspologic.simulations import er_nm, er_np
n = 50
m = 250
p = 0.3
np.random.seed(1)
G1 = er_np(n=n, p=p)
G2 = er_nm(n=n, m=m)
Visualize the graphs using heatmap¶
[3]:
from graspologic.plot import heatmap
heatmap(G1, title = 'ER-NP(50, 0.3) Simulation')
_ = heatmap(G2, title = 'ER-NM(50, 250) Simulation')

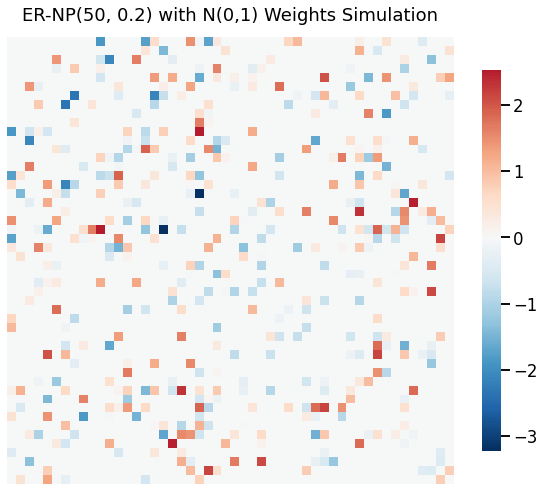
Weighted ER Graphs¶
Both er_np() and er_nm() functions provide ways to sample weights for all edges that were sampled via a probability distribution function. In order to sample with weights, we provide a probability distribution function with corresponding keyword arguments for the distribution function.
Below we sample \(G_1 \sim ER_{NP}(50, 0.2)\) where the weights are distributed normally with \(\mu = 0,~\sigma^2 = 1\).
[4]:
wt = np.random.normal
wtargs = dict(loc=0, scale=1)
G1 = er_np(n=50, p=0.2, wt=wt, wtargs=wtargs)
Visualize the graph using heatmap¶
[5]:
_ = heatmap(G1, title = 'ER-NP(50, 0.2) with N(0,1) Weights Simulation')